Курсовая работа: Дистанційна слідкуюча система на сельсинах
З графіків видно, що робота системи залежить від вхідного сигналу.
4. Аналіз дискретної САК (ДСАК)
В основі аналізу дискретної САК візьмемо лінійну неперервну САК після корекції з передаточною характеристикою
w(s) = 
.
4.1 Визначення періоду дискретизації імпульсного елемента
В якості формоутворювача сигналу приймемо екстраполятор нульового порядку.
ωз = 125с-1 – максимальна частота в спектрі вхідного сигналу.
За теоремою Котельникова для нормальної роботи системи необхідно, щоб виконувалася умова Tk = 
- період дискретизації, відповідно ωк ≥ 2ωз – частота дискретизації. Оберемо ωк ≥ 3·125 = 375 с-1 , тоді Tk ≤ 
(с).
Виберемо період дискретизації Tk = 0,006с, ωк = 628 с-1 .
4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії
w(z) = 
.
Спочатку розкладемо функцію на простіші дроби:
.
Виконаємо z-перетворення Лапласа отриманої функції:
.
Отже,
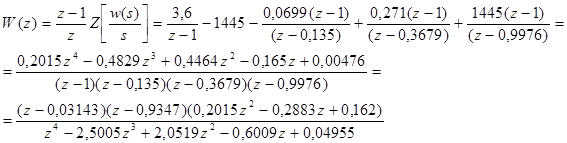
Передатна функція замкненої ДСАК:
.
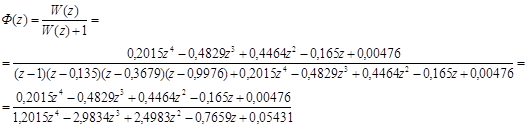4.3 Визначення стійкості отриманої системи по критерію Гурвіца
Знаючи перехідну функцію, знайдемо характеристичне рівняння системи:D(s)=
.
Виконаємо білінійне перетворення 
.
Отримаємо наступне характеристичне рівняння:
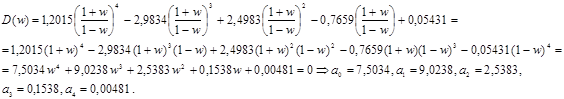
На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:
D =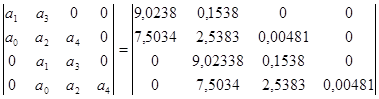 
.
За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а0 >0 всі визначники Гурвіца були додатними.
а0 =7,5034>0,
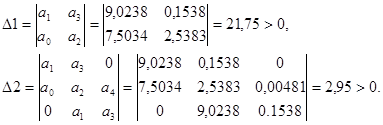
Умова стійкості системи виконуються, отже за критерієм Гурвіца САК стійка .
4.4 Побудова логарифмічної псевдочастотної характеристики ДСАК та визначення запасів стійкості
Для побудови логарифмічної псевдочастотної характеристики використаємо передаточну функцію розімкненої системи після корекції та виконання z- перетворення:
