Курсовая работа: Дистанційна слідкуюча система на сельсинах

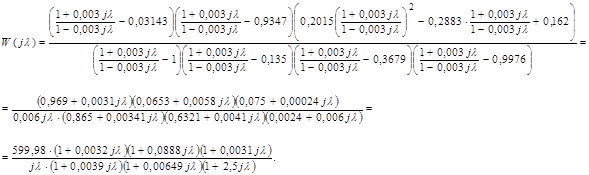
Знайдемо нульову контрольну точку: L₀ = 20lgk = 20lg599,98 = 55,6 дБ.

Визначимо спряжені частоти:

λ₁ = = 256с^-1 , λ₂ = = 154с^-1 ,

λ₃ = = 0,4с^-1 , λ₄ = = 312,5с^-1 , λ₅ = = 11с^-1 ,

λ₆ = = 322,6с^-1 .

Враховуючи, що до складу системи входить пропорційна, інтегруюча, три аперіодичні ланки першого порядку та три форсуючі ланки отримуємо ЛАХ і ЛФХ для даної САК (рис. 17).

Рис. 17. Логарифмічні частотні характеристики системи.

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

· по амплітуді запас стійкості h=µ (DL), тому що ЛФХ не перетинає межу -p.

· по фазі: Δφ = π-Arg(w(j*ω_з )), де ω_з – частота зрізу, коли L(ω_з ) = 1, тобто

ω_з = 8. Тоді Δφ = arg(w(j*8) = -38°.

4.5 Розрахунок та побудова графіку перехідної характеристики ДСАК

Для побудови перехідної характеристики ДСАК використаємо перехідну характеристику замкненої системи отриману раніше.

Розрахуємо перехідну характеристику ДЦСАК Y(z) = Ф(z)*G(z), де G(z) = - зображення вхідного одиничного сигналу. Тобто

.

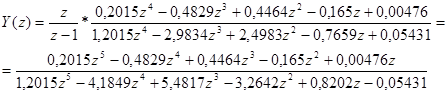Побудуємо графік перехідного процесу, попередньо розклавши перехідні характеристики в ряд Лорана:

_

_

_

_

_