Курсовая работа: Дослідження збіжності рішень для диференціальних рівнянь у частинних похідних, отриманих методом сіток

Апроксимуємо часткові похідні відповідними різницями:

.

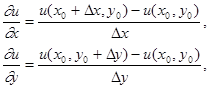
Аналогічно можна записати

тобто різницю зміщаємо до центра

Формула для змішаної похідної

Ці формули переходу до різницевих схем можна записати, використовуючи позначення:

,

,

.

Скористаємося розкладанням у ряд Тейлора:

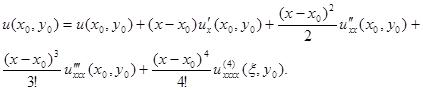
Для того, щоб оцінити похибку 2-ої похідної заміняємо в першій заміні, у другій заміні .

Отже, для

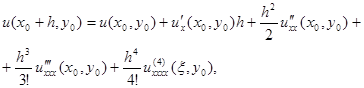
а для

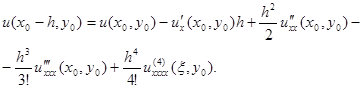
Користуючись цими розкладаннями, одержимо

Аналогічну формулу можна записати для похідної по у.

.