Курсовая работа: Дослідження збіжності рішень для диференціальних рівнянь у частинних похідних, отриманих методом сіток

для граничних вузлів

р=0,1,2,…,задане.

Доведено, що якщо gi,k<0, то послідовні наближення збігаються до точного розв’язку різницевої схеми ui,k або системи рівнянь (14), (15) і має місце оцінка

max

i,k i,k

де q=max .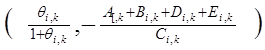

i,k

Доведенняцьоготвердженняполягаєвперевірціумовизбіжностіметодупростоїітераціїдлясистемилінійнихрівнянь, прицьомумаєтьсянаувазі, щоневідомийвекторутворюєелементи ui,k. Наприклад, компонентивектораможнаперенумеруватитакимчином: нехайтоді

x1= u1.1, x 2 =u 2.1,…, x N1 = u N1.1;

x N1+1=u 2.1 x N1+2 =u 2.2,…, x 2N1 =u N1.2;

…………………………x N1N2 =u N1N2.

Відносно вектора = різницева схема є системою лінійних рівнянь в матричному записі де матриця А має в кожному рядку не більше п’яти елементів

.........

........

А=... ... .. ...

... ... .. ...

.........

Це пов’язано з тим, що похідні в кожному внутрішньому вузлі (i,k) апроксимувались за п’ятьма сусідніми вузлами.

Розв’язання різницевих рівнянь при h 0 збігається до точного розв’язання крайової задачі зі швидкістю, яка визначається порядком апроксимації рівнянь та крайових умов. Таким чином, для точного розв’язання (u(x,y)) оцінки похибки

max O(h2), h 0 (16)

i, k

Оцінка похибки (16) є справедливою, якщо точний розв’язок неперервно диференційований чотири рази в області G. Для областей з кутовими точками, наприклад прямокутника, взагалі кажучи, u(x,y) . Але якщо гранична функція, тобто задовольняє в кутах спеціальні умови узгодження, то точний розв’язок u(x,y) і є вірною оцінка (16).

Для прямокутної області G= такими умовами узгодження можуть бути:

достатня гладкість ;

функція повинна задовольняти в кутах прямокутника диференціальне рівняння.

Оцінка похибки (8.96) має в основному теоретичне значення, оскільки містить константу С, яку практично важко визначити

max ch2+ O(h2), h 0