Курсовая работа: Дослідження збіжності рішень для диференціальних рівнянь у частинних похідних, отриманих методом сіток

Знайти чисельно розв'язок у(х) в усіх точках відрізка [а;b] неможливо, оскільки їх безліч. Тому на відрізку [а;b] беруть скінчену кількість точок (хі = a+ih, i = 0,1.....п, а + пh<=b<a +(п + 1)h) і тільки

в них знаходять значення у(х). Початкове значення y(a)=y0 нам відоме. Для знаходження інших значень уi= у(хі) (i = 1,2,.., n) диференціальне рівняння розглядають не на всьому відрізку [a;b], а тільки в зазначених точках y’(xi)=f(xi,y(xi)).

Замінивши похідну у'(х) її наближеним значенням (уi+1 - уі)/h, дістають систему рівнянь

уi+1 - уі= пf(хі, уі), i = 0,1,2,...,n-1. (20)

Звідси послідовно знаходять y1, y2,… yn.

Якщо в рівняння (20) замість уi i уi+1 підставити точні значення розв'язку у(хi) і y(xi+i)> то рівності задовольняться лише наближено.

Похибку, яку дістають від заміни неперервної моделі дискретною, називають похибкою дискретизації (або похибкою апроксимації),

Крім похибки дискретизації, існує інший тип похибки чисельних методів. В основі багатьох методів лежить ідея ітераційного процесу, в ході якого будується за певним правилом послідовність наближень до розв'язку задачі. Якщо ця послідовність має границю, коли кількість членів послідовності прямує до нескінченності, тоді ця границя буде розв'язком даної задачі. Але на ЕОМ можна обчислити тільки скінчену кількість членів послідовності. Похибку, спричинену обривом ітераційного процесу, називають похибкою збіжності. Похибку методу намагаються звести до величини, яка в кілька разів менша від похибки вхідних даних.

Отже, похибку чисельного методу можуть утворювати похибки дискретизації або похибки збіжності, або ж для деяких методів обидва типи похибок одночасно. Всі ці похибки, а також методи їх аналізу і регулювання розглядаються при побудові конкретних чисельних методів.

Обчислювальні похибки пов'язані з похибками округлення чисел. Обчислення, як ручні, так і на ЕОМ, виконують з певною кількістю значущих цифр. Це вносить у, результат похибку округлення, яка нагромаджується в ході обчислень. Похибки округлення можуть по-різному впливати на кінцевий результат. У результаті виконання мільйонів операцій, кожна з яких вносить невелику похибку, сумарна похибка округлень може значно перевищити шуканий результат обчислень. Але в окремих операціях похибки округлень можуть мати різні знаки і частково компенсувати одна одну. Тому, якщо немає систематичних причин, випадкове нагромадження похибок округлення незначне.

Систематичною причиною нагромадження похибок є, наприклад, віднімання близьких за величиною чисел, оскільки при малій абсолютній похибці чисел х1 і х2 відносна похибка (∆x1+∆x2)/|x1-x2| результату може стати великою.

Обчислювальні похибки виникають і під час перетворення чисел з однієї системи числення в іншу, якщо основа однієї системи числення не є степенем основи іншої. Це може призвести до того, що в новій системі числення число стане ірраціональним.

Втрата точності може статися і при додаванні до великого числа дуже малих чисел. Для зменшення похибки додавати числа варто в порядку їх зростання. У машинній арифметиці комутативний і дистрибутивний закони алгебри не завжди виконуються. Обчислювальний алгоритм треба будувати так, щоб похибка округлень була значно меншою від усіх інших похибок.

Поняття стійкості та коректності

Похибки у вхідних даних задачі — неусувні. Обчислювач не може їх зменшити, але мусить знати, як вони впливають на точність кінцевого результату. Одні задачі мають похибку результату такого самого порядку, як і порядок похибки вхідних даних, в інших задачах похибка результату може на кілька порядків перевищувати похибку вхідних даних. Чутливість задачі до неточностей у вхідних даних характеризується поняттям стійкості.

Задача називається стійкою за вхідними даними, якщо її розвязок неперервно залежить від вхідних даних, тобто малому приросту ∆х вхідної величини відповідає малий приріст ∆у шуканого розв'язку. Іншими словами, малі похибки вхідних даних спричинюють малі похибки розв'язку задачі. Якщо ця умова не виконується, то задача вважається нестійкою за вхідними даними. Це означає, що навіть незначні похибки вхідних даних можуть привести до як завгодно великих похибок розв'язку, тобто розв'язок може бути зовсім спотворений. Тому застосовувати безпосередньо до таких задач чисельні методи не можна, оскільки похибки округлень при застосуванні методу будуть катастрофічно нагромаджуватись у ході обчислень. Наведемо приклад нестійкої задачі, який належить Уілкінсону.

Введемо тепер поняття коректності задачі.

Задача називається коректно поставленою, якщо для будь-яких вхідних даних з деякого класу існує єдиний і стійкий за вхідними даними її розв'язок.

Для розв'язування некоректно поставлених задач застосовувати класичні чисельні методи не варто, оскільки похибки округлень при розрахунках можуть катастрофічне зростати і призвести до результату, далекого від шуканого розв'язку. Для розв'язування некоректно поставлених задач використовують так звані методи регуляризацїї, які замінюють дану задачу коректно поставленою.

Програмна реалізація

Розглянемо приклад рівняння в частинних похідних гіперболічного типу

Область:

Початкові умови:

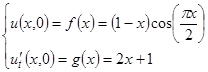
Граничні умови:

Крок по осі Х: hx=0,1

Крок по осі Y: hy=0,05