Курсовая работа: Электростатика проводников

Эти формулы показывают, что, дифференцируя энергию U по величинам зарядов, мы получаем потенциалы проводников, а производные от U по потенциалам дают значения зарядов:

проводник электромагнитный поле выравнивание

.

С другой стороны, потенциалы и заряды являются линейными функциями друг друга. Имеем:

,

а изменив порядок дифференцирования. Мы получили бы . Отсюда видно, что

(и, аналогично, ). Энергия Uможет быть представлена в виде квадратичной формы потенциалов или зарядов:

.

Это квадратичная форма должна быть существенно положительной. Из этого условия возникают определенные неравенства, которым удовлетворяют коэффициенты . В частности, все коэффициенты емкости положительны:

(а также и ).

Напротив, все коэффициенты электростатической индукции отрицательны:

.

3. Проводящий эллипсоид

Задача об определении заряженного проводящего эллипсоида решается с помощью эллипсоидальных координат.

Связь эллипсоидальных координат с декартовыми дается уравнением

Это уравнение, кубическое относительно u, имеет три вещественных корня :

.

Эти три корня и являются эллипсоидальными координатами точки x, y, z. Их геометрический смысл явствует из того, что поверхности постоянных значений представляют собой соответственно эллипсоиды, однополостные гиперболоиды и двухполюсные гиперболоиды, причем все они софокусны с эллипсоидом

.

Формулы преобразования от эллипсоидальных координат к декартовым получаются путем совместного решения трех уравнений и имеют вид

,

,

.

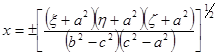Элемент длины в эллипсоидальных координатах имеет вид

,

,
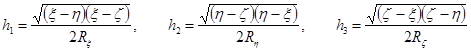