Курсовая работа: Электростатика проводников

Соответственно, уравнение Лапласа в этих координатах есть

Тогда кубическое уравнение

вырождается в квадратное

с двумя корнями, пробегающими значения в интервалах

Координатные поверхности постоянных и превращаются соответственно в софокусные сплюснутые эллипсоиды вращения и однополостные гиперболоиды вращения (рис. 1). В качестве третьей координаты можно ввести полярный угол в плоскости

.

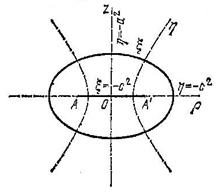
Рис. 1

Связь координат с координатами дается равенствами

, .

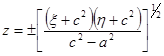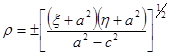Координаты называются сплюснутыми сфероидальными координатами.

При a>b=с эллипсоидальные координаты вырождаются в так называемые вытянутые сфероидальные координаты. Две координаты и задаются корнями уравнения

причем . Поверхности постоянных и представляют собой вытянутые эллипсоиды и двуполостные гиперболоиды вращения (рис. 2).

Связь координат , с координатами дается формулами

, .

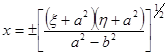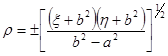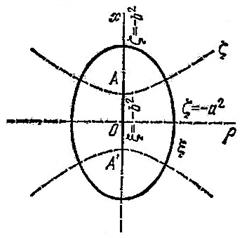
Рис. 2

Поверхность

в эллипсоидальных координатах – это координатная поверхность =0. Если искать потенциал поля в виде функции только от , то будут эквипотенциальными все эллипсоидальные поверхности =const, в том числе поверхность проводника. Уравнение Лапласа сводится тогда к уравнению

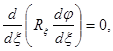
откуда

.
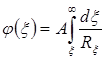