Курсовая работа: Генерация матриц

Курсовая работа

"Генерация матриц"

Введение

В настоящее время матричное исчисление широко применяется в различных областях математики, механики, теоретической физики, теоретической электротехники и т.д.

Целью курсовой работы является разработка алгоритма и написание на его основе программы, которая генерирует квадратную матрицу по ее введенному определителю, размерности и диапазона элементов матрицы.

Данная курсовая работа состоит двух глав, включающих в себя каждая несколько параграфов и подпунктов.

В первой главе приведена теоретическая часть по генерации матриц, включающая основные понятия и определения теории матриц, основные теоремы теории матриц, дающие научную основу для разработки алгоритма генерации матриц и написании на его основе программы. Здесь вводятся основные операции над матрицами и детально изучаются свойства определителей, являющихся основой числовой характеристикой квадратных матриц.

Во второй главе рассказывается об основных проблемах, с которыми столкнулся при составлении алгоритма и написании программы, приводится алгоритм генерации матриц, описываются некоторые важные части программы, основывающейся на алгоритме, и приводится листинг программного продукта.

В заключении говорится о проблемах, с которыми столкнулся при составлении алгоритма и написании на его основе программы, и о путях усовершенствования предложенного алгоритма и программы.

1. Матрицы и определители

1.1 Матрицы. Действия с матрицами

Все определения, теоремы, свойства, следствия и их доказательства, используемые в курсовой работе, взяты из книги В.А. Ильина, Э.Г. Позняка «Линейная алгебра».

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов (размера ).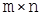

Числа m и n называются порядками матрицы. Если m=n, матрица называется квадратной , а число m=n – её порядком .

Для записи матрицы применяются либо сдвоенные черточки, либо круглые или квадратные скобки:

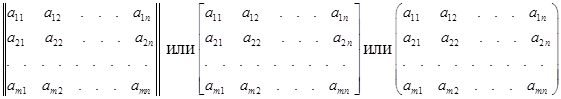
Для краткого обозначения матрицы часто используется либо одна большая латинская буква (например, A), либо символ , либо .

Числа , входящие в состав данной матрицы, называются её элементами .В записи первый индекс означает номер строки, а второй индекс – номер столбца.

В случае квадратной матрицы

(1.1)

вводится понятия главной и побочной диагоналей. Главной диагональю матрицы называется диагональ a ₁₁ a ₂₂ … a_{n n} , идущая из левого верхнего угла этой матрицы в правый нижний её угол. Побочной диагональю матрицы называется диагональ a_{n 1} a _{( n - 1)2} … a _{1 n ,} идущая из левого нижнего угла в правый верхний угол.

Прежде всего, будем считать две матрицы равными , если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают.

Перейдём к определению основных операций над матрицами.

Сложение матриц .Суммой двух матриц и одних и тех же порядков m и n называется матрица тех же порядков m и n , элементы c_{i j} которой равны

(1.2)

Для обозначения суммы двух матриц используется запись C=A+B. Операция составления суммы матриц называется их сложением .

Итак, по определению

=

=

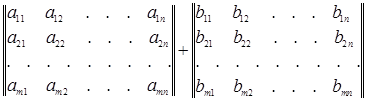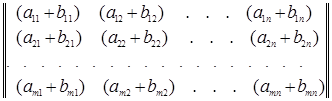
Из определения суммы матриц, а точнее из формулы (1.2) непосредственно вытекает, что и операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно:

1) переместительным свойством: A+B=B+A,

2) сочетательным свойством: (A+B)+C=A+(B+C).

Эти свойства позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--