в) Якщо b>a, але b<a √2, то OM<2a² -b² <a² , тобто OM< і, тим більше, отже, коло, описане з центра О радіусом ОМ, перетинає відрізок АВ.

г) Якщо b=a√2, то 2а² -b² =0, тобто ОМ=0, і геометричне місце точок перетворюється в точку О.

д) Якщо b>a√2, то 2а² -b² <0 і задача не має розв’язку.

Обернена теорема. Будь-яка точка М кола, описаного зсередини О даного відразка АВ, як з центра, радіусом де а – даний відрізок, задовольняє умову МА² +МВ² =а² .

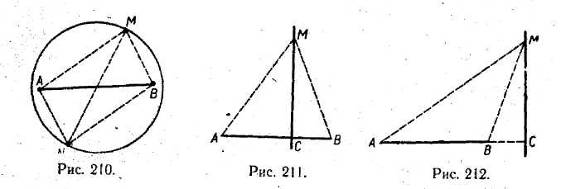
Дані точки А і В, де АВ=b, відрізок а і коло, описане з середини О відрізка АВ, як з центрра, радіусом (рис. 210).

Треба довести, що будь-яка точка М побудованого кола відповідає умові: МА² + МВ² = а² .

Проводимо діаметр MN і будуємо паралелограмм MANB, з якого маємо: 2MA² + 2MB² = AB² + MN² , тобто MA² + MB² = a² , бо MN² = 2a² – b² , aAB² = b² .

ХІ. Геометричне місце точок таких, що різниця квадратів їх віддалей від двох даних точок А і В дорівнює квадратові даного відрізка а (тобто а² ), є пряма, перпендикулярна до прямої АВ в такій внутрішній або зовнішній точці С відрізка АВ, що СА² -СВ² =а² .

Доведемо теорему про дане геометричне місце точок.

Теорема 247. Будь-яка точка М, що має відносно даних точок А і В властивість: МА² – МВ² = а² , де а – даний відрізок, лежить на прямій, перпендикулярній до прямої АВ, і перетинає відрізок АВ в такій точці С, що СА² – СВ² = а² .

Дані точки А і В і відрізок а: приймемо, що точка М задовольняє умову: МА² – МВ² = а² (рис. 211 і 212).

Опустимо з точки М перпендикуляр на пряму АВ і доведемо, що точка С перетину проведеного перпендикуляра з прямою АВ задовольняє умову: СА² – СВ² = а² .

З прямокутних трикутників МАС і МСВ маємо: МА² = СА² + МС² і МВ² = СВ² + МС² , тобто МА² – МВ² = СА² – СВ² , або СА² – СВ² = а² , що й треба було довести.

Зауваження 1. Коли дані точки А та В і відрізок а, то для того, щоб побудувати точку М, яка мала б властивість МА² + МВ² = а² , на даному відрізку KLP = a, як на катеті, будуємо будь-який прямокутний трикутник KLP (рис. 213), але такий, щоб КР + LP було більше за відрізок АВ.

Коли з точки А, як з центра, опишемо дугу радіусом LP, а з точки В-дугу радіусом КР, то знайдемо точку М, що задовольняє умову МА² – МВ² = а² .

Перпендикуляр МС до прямої АВ і буде шуканим геометричним місцем (рис. 214).

Зауваження 2. а) Якщо МА² < MB² + AB² , тобто, якщо АВ² >МА² – МВ² , або АВ² > a² і АВ² > a, то – гострий і точка С лежить на відрізку АВ (рис. 211).

б) Якщо МА² = МВ² + АВ² , тобто, якщо АВ² = а² , або АВ = а, то - прямий і точка С зливається з точкою В.

в) Якщо МА² > MB² + AB² , тобто, якщо AB² < MA² – MB² , або AB² < a² і АВ < а, то - тупий і точка С лежить поза відрізком АВ (рис. 212).

Теорема 248. Будь-яка точка М прямої МС, перпендикулярної до даної прямої АВ і такої, що проходить через таку внутрішню або зовнішню точку С відрізка АВ, що СА² – СВ² = а² , де а – даний відрізок, задовольняє умову МА² – МВ² = а² .

Дані точки А і В, відрізок а і пряма МС, перпендикулярна до прямої АВ і така, що перетинає її в точці С всередині відрізка АВ (рис. 211) або поза відрізком АВ (рис. 212), причому СА² – СВ² = а² .

Доведемо, що будь-яка точка М, яка лежить на перпендикулярні МС, задовольняє умову МА² – МВ² = а² . З прямокутних трикутників МАС і МВС (рис. 211 і 212) маємо:

СА² = МА² – МС² і СВ² = МВ² – МС² .

тобто:

МА² – МВ² = СА² – СВ² , або МА² – МВ² = а² .

що й треба було довести

4. Застосування ГМТ до розв’язання задач на побудову

геометричний площина точка місце