Якщо покласти v _i = g(x _i ) (i = 0, 1, . . ., n ), то будемо мати

v ₀ <v ₁ < ... <v _i < v _{i +1} < ... <v_n = V .

Так як х _i = g ^-1 (v _i ) , то

Цей вираз має вигляд ріманової суми для інтеграла

Маємо

і

так що

Припустимо тепер настільки малими, щоб коливання функції f(x) у всіх проміжках [x_і , х_і+1 ] були менше довільно наперед заданого числа > 0. Так як при , очевидно, , то одночасно і <.

В такому випадку

<

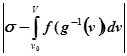Цим доведено, що

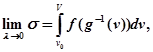
звідки и слідує (10). [4;6]

§6. Обчислення інтегралів Стілтьєса

Доведемо наступну теорему:

1. Якщо функція f(x) інтегрована в сенсі Рімана на проміжку [a, b], a g(x) представлена інтегралом

де функція абсолютно інтегровна в [а, b ], то

(11)

Існування інтеграла Стілтьєса при зроблених припущеннях уже було доведено вище.

Залишається лише з’ясувати рівність (11).

Без зменшення загальності можна припустити, що функція додатна.

Складемо суму Стілтьєса

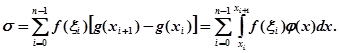
Так як, з іншого боку, можна написати

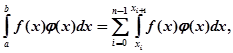
то будемо мати

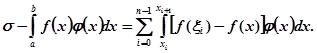
Очевидно, для буде , де означає коливання функції f(x) на проміжку [x_і , x_і+1 ]. Звідси витікає така оцінка записаної вище різниці:

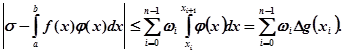
Нам відомо, що при остання сума прямує до 0, з чого слідує, що

,

що і доводить формулу (11).

2. При тих самих припущеннях стосовно функції f(x) припустимо, що функція g(x) неперервна на всьому проміжку [а, b ] і має в ньому, за виключенням лише скінченої кількості точок, похідну g'(x), яка на [а, b ] абсолютно інтегрована. Тоді

(12)

Звертаючись до випадків, коли функція g ( x ) є розривною розглянемо спочатку «стандартну» розривну функцію р(х) , яка визначається рівностями

Вона має розрив першого роду — стрибок — у точці х = 0 зправа, причому величина стрибка р(+0) – р(0)) дорівнює 1; в точці х =0 зліва і в решті точок функція p ( x ) неперервна. Функція p ( x – c ) буде мати такий самий розрив у точці x = c зправа; навпаки, p ( с – x ) буде мати подібний розрив у точціx = c зліва, причому величина стрибка дорівнює – 1.

Припустимо, що функція f(x) неперервна в точці х = с , і обчислимо інтеграл , де (при інтеграл рівний нулю).

Складемо суму Стілтьєса:

.

Нехай точка потрапляє, скажімо в -ий проміжок, так що . Тоді , а при , очевидно . Таким чином, уся сума зводиться до одного доданку . Нехай тепер . По неперервності . Виходячи з цього, існує (при )

(13)