Курсовая работа: Измеримые функции
Функция f(x), заданная на сегменте [а, b], называется ступенчатой, если [а,b] разложить точками.
с0 = а< с1 <с2 <…<сn = b
на конечное число частей, в н у т р и которых (т.е. в интервалах (сk , ck + 1 ) при k = 0, 1, …., n –1) функция f(x) постоянна . Легко понять, что из теоремы 5 вытекает
Следствие . Ступенчатая функция измерима.
Теорема 6. Если f ( x ) есть измеримая функция, заданная на множестве Е, то при любом а измеримы множества
E (f ³ a), E (f = a), E (f £ a), E (f < a),
Д о к а з а т е л ь с т в о. Легко проверить, что
E (f ³ a) = 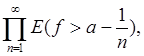
откуда следует измеримость множества E (f³ a). Измеримость прочих множеств вытекает из соотношений:
E (f = a) = E(f ³ a) – E(f > a), E(f £ a) = E – E(f > a),
E (f < a) = E – E (f ³ a).
Замечание. Легко показать, что если хоть одно из множеств
E (f ³ a), E (f £ a), E (f < a)
оказывается измеримым при всяком а, то функция f ( x ) измерима на множестве Е (которое также предполагается измеримым).
Действительно, тождество 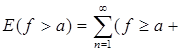
![]() ) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).
) показывает, например, что f(x) измерима, если измеримы все множества Е (f³а). Сходным образом устанавливаются и остальные утверждения. Таким образом, в определении измеримой функции можно заменить множество Е (f>a) любым из множеств (1).
Теорема 7. Если функция f ( x ), заданная на множестве Е, измерима, а k конечное число, то измеримы и функции 1) f ( x ) + k , 2) kf ( x ), 3) ç f ( x ) ç , 4) f 2 ( x ), и если f ( x ) ¹ 0, то измерима и функция 5) ![]() .
.
Д о к а з а т е л ь с т в о . 1) Измеримость функции f(x) +k вытекает из соотношения Е (f+k>a) = E (f>a- k).
2) Измеримость функции kf(x) при k =0 следует из теоремы 5. Для прочих kизмеримость следует из очевидных соотношений

3) Функция çf(x) ç измерима потому, что

4) Аналогично, из того , что
E (f2 > a) =
вытекает измеримость функции f 2 (x).
5) Наконец, при f(x) ¹ 0 имеем
![]() > a) =
> a) = 

откуда и следует измеримость ![]() .
.
Теорема 8 . Функция f ( x ), заданная и непрерывная на сегменте Е= ![]() , измерима.
, измерима.
Д о к а з а т е л ь с т в о. Прежде всего установим, что множество
F = E (f£ a)
замкнуто. Действительно, если x0 есть предельная точка этого множества и xn ®x0 (xn ÎF ), то f(xn ) £aи, в силу непрерывности f(x), будет f(x0 ) £a, т.е. x0 ÎF, что и устанавливает замкнутость множества F.
Но тогда множество Е (f>а) = Е – Е(f£а) измеримо, и теорема доказана.
Из самого определения измеримой функции следует, что функция, заданная на неизмеримом множестве, неизмерима.
Однако легко обнаружить существование неизмеримой функции, заданной на измеримом множестве.
Определение 4. Пусть М есть подмножество сегмента Е = [А, В]. Функция jм (х), равная единице на множестве М и нулю на множестве Е–М, называется характеристической функцией множества М.
Теорема 9. Множество М и его характеристическая функция j м одновременно измеримы или нет.
Д о к а з а т е л ь с т в о. Если функция jM (х) измерима, то измеримость множества М вытекает из соотношения
М = Е (jм > 0).
Обратно, если М есть измеримое множество, то соотношения

устанавливают измеримость функции jМ (х).
Отсюда, между прочим, весьма просто получаются примеры разрывных измеримых функций.
Дальнейшие свойства измеримых функций
Лемма. Если на множестве Е заданы две измеримые функции f (х) и g (х), то множество Е ( f > g ) измеримо.
Действительно, если мы перенумеруем все рациональные числа r1, r2 , r3 , …, то легко проверим справедливость соотношения
Е (f > g) = ![]() Е (f > rk ) Е (g < rk ),
Е (f > rk ) Е (g < rk ),
откуда и следует лемма.
Теорема 1. Пусть f (х) и g (х) суть конечные измеримые функции, заданные на множестве Е. Тогда измерима каждая из функций 1) f (х) – g (х), 2) f (х) + g (х), 3) f (х) . g (х), и если g (х) ¹ 0, то измерима также функция 4) ![]()
![]() .
.