Курсовая работа: Измеримые функции

В самом деле, если , то , причем все числа f₁ (x₀ ), f₂ (x₀ ), … и их предел f (x₀ ) – конечны. Значит найдется такое n, что для k³ n будет |f_k (x₀ ) – f(x₀ ) < s.

Иначе говоря (k³ n), а потому и тем более , откуда и следует (3).

Но тогда, в силу (1), nM=0, и (2) принимает вид

(4)

Этим и доказана теорема, ибо Е_n (s) ÌR_n (s).

Замечание . Отметим, что нами установлен результат (4), более сильный, чем то, что мы хотели доказать. Ниже при доказательстве теоремы Д.Ф. Егорова, нам придется воспользоваться именно этим более сильным результатом.

Доказанная теорема дает повод установить следующее

Определение. Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций

f₁ (x), f₂ (x), f₃ (x), …

и измеримая и почти везде конечная функция f(x). Если, каково бы ни было положительное число s, оказывается, что

,

то говорят, что последовательность (^* ) сходится к функции f ( x ) по мере.

Мы будем, следуя Г.М.Фихтенгольцу, обозначать сходимость по мере символом

f_n (x) Þ f(x).

С помощью понятия сходимости по мере можно формулировать теорему Леберга так.

Теорема 1*. Если последовательность функций сходится почти везде, то она сходится и по мере к той же предельной функции.

Следующий пример показывает, что эта теорема необратима.

П р и м е р . Определим на полусегменте [0, 1) для каждого натурального k группу из k функций: f₁ ^{( k )} (x), f₂ ^{( k )} (x), …, f_k ^{( k )} (x), полагая

В частности, f₁ ⁽¹⁾ (x) º 1 на [0, 1). Нумеруя все построенные функции подряд одним значком, мы получим последовательность

j₁ (x) = f₁ ⁽¹⁾ (x), j₂ (x) = f₁ ⁽²⁾ (x), j₃ (x) = f₂ ⁽²⁾ (x), j₄ (x) = f₁ ⁽³⁾ (x), …

Легко видеть, что последовательность функций j_n (x) сходится по мере к нулю. В самом деле, если j_n (x) = f_i ^{( k )} (x), то при любом s>0 будет

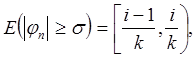
и мера этого множества, равная 1/k, стремится к нулю с возрастанием n.

Вместе с тем, соотношение j_n (x)®0 не выполняется ни в одной точке промежутка [0, 1). Действительно, если 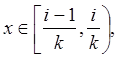так что f_i ^{( k )} (x₀ ) = 1. Иначе говоря, как далеко мы не продвинемся вдоль ряда чисел j₁ (x₀ ), j₂ (x₀ ), j₃ (x₀ ), …, мы всегда будем встречать в этом ряду числа, равные 1, что и доказывает наше утверждение.

Таким образом, понятие сходимости по мере есть понятие, существенно более общее, чем понятие сходимости почти везде и тем более, чем понятие сходимости везде.

Естественно спросить, в какой степени соотношение

f_n (x) Þ f(x)

определяет функцию f(x), т.е. единственна ли предельная функция при сходимости по мере.

Теоремы 2 и 3 позволяют ответь на этот вопрос.

Теорема 2. Если последовательность функций f_n ( x ) сходится по мере к функции f ( x ), то эта же последовательность сходится по мере ко всякой функции g ( x ), эквивалентной функции f ( x ).

Д о к а з а т е л ь с т в о. При любом s > 0 будет

E( êf_n – gê³s ) ÌE( f ¹g) + E( çf_n - fç³s),

откуда (поскольку mE (f¹g) = 0)

mE (êf_n – gê³s) £mE(çf_n – fç³s),

что и доказывает теорему.

Теорема 3 . Если последовательность функций f_n ( x ) сходится по мере к двум функциям f ( x ) и g ( x ), то эти предельные функции эквивалентны.

Д о к а з а т е л ь с т в о. Легко проверить, что при s > 0 будет

(*)

ибо точка, не входящая в правую часть этого соотношения, и подавно не может входить и в левую часть. Но соотношения

f_n Þ f, f_n Þ g