Курсовая работа: Измеримые функции

то f ~g, что и требовалось доказать.

Теоремы 2 и 3 показывают, что, желая восстановить свойство единственной предельной функции для сходимости по мере, мы должны были бы условиться считать эквивалентные функции за тождественные. Это обычно и делается в метрических вопросах теории функций, т.е. в тех вопросах, где все свойства функций изучаются с помощью меры множеств, на которых функция обладает или не обладает тем или другим свойством. В интегральном исчислении мы надем много примеров подобного подхода к вещам.

Хотя сходимость по мере общее сходимости почти везде, имеет место все же следующая теорема.

Теорема 4 (Ф.Рисс). Пусть { fn ( x )} последовательность функций, которая сходится по мере к функции f ( x ). В таком случае существует подпоследовательность

fn₁ (x), fn₂ (x), fn₃ (x), ... (n₁ <n₂ <n₃ <...),

сходящаяся к функции f ( x ) почти везде.

Д о к а з а т е л ь с т в о. Возьмем последовательность положительных чисел s₁ >s₂ >s₃ >¼, для которой lims_k =0.

Пусть, далее, h₁ +h₂ +h₃ +¼ (h_k >0) есть сходящийся положительный ряд.

Теперь мы можем построить требуемую последовательность индексов

n₁ < n₂ < n₃ < ... (*)

следующим образом: обозначим через n₁ натуральное число, для которого

mE(½f_n1 -f½³s₁ )<h₁ .

Такое число обязательно существует, ибо

mE(½f_n -f½³s₁ )®0 при n®¥.

Затем через n₂ обозначим то натуральное число, для которого

mE(½f_{n 2} -f½³s₂ )h₂ ,n₂ >n₁ .

Вообще через n_k мы обозначаем такое число, что

mE(½f_nk -f½³s_k )< h_k , n_k >n_k-1 .

Последовательность (*), таким образом, построена.

Теперь установим, что почти везде на множестве E будет

(**)

Действительно, пусть

, .

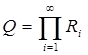Так как R₁ ÉR₂ ÉR₃ É..., то (теорема 12)

mR_i ®mQ

C другой стороны, очевидно, что 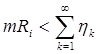так что mR_i ®0 и, стало быть, mQ=0.

Остается проверить, что соотношение (**) имеет место для всех x из множества E - Q.

Пусть x₀ ÎE - Q. Тогда x₀ R_io . Иначе говоря, при k³i₀

x₀ E(|f_nk -f|³s_k ),

и, следовательно,

|f_nk (x₀ ) – f(x₀₎ |<s_k , (k³i₀ )

и, поскольку s_k ®0, ясно, что f_nk (x₀ ) ®f(x₀ ).

Теорема доказана.

Теорема Лебега дала повод к установлению понятия сходимости по мере. С другой стороны, с помощью этой же теоремы можно установить весьма важную теорему Д.Ф.Егорова.

Теорема 5 (Д.Ф.Егоров). Пусть на измеримом множестве Е задана последовательность измеримых и почти везде конечных функций f ₁ ( x )^, f ₂ ( x )^, f ₃ ( x ), …, почти везде сходящаяся к измеримой и почти везде конечной функции f ( x ):

В таком случае, для любого d >0 существует такое измеримое множество Е _d Е, что:

1) mE _s > mE - d ;

2) на множестве E _d стремление(*) происходит равномерно.

Д о к а з а т е л ь с т в о. При доказательстве теоремы Лебега было установлено, что при любом s >0 будет

(1)

где .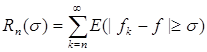

Заметив это, возьмем сходящийся положительный ряд

h₁ +h₂ +h₃ +... (h_i >0)