Курсовая работа: Измеримые функции

В силу (1), можно каждому натуральному i соотнести такое натуральное n_i , что mR_ni (s_i )< h_i .

Сделав это, найдем такое i₀ , что 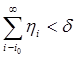(где d число, фигурирующее в формулировке теоремы), и положим .

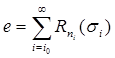Очевидно,

me<d.

Пусть Е_d = Е – е. Установим, что множество Е_d требуемое. Неравенство mE_d > mE - d ясно, так что остается убедиться в равномерности стремления

f_n (x)®f(x)

на множестве Е_d .

Пусть e > 0. Найдем i такое, что i³i₀ , s_i < e, и покажем, что при k³ n_i и при всех xÎ Е_d будет

|f_k (x) – f(x)| < e,

откуда и будет следовать теорема.

Если xÎ Е_d , то хe. Значит в частности, xR_ni (s_i ).

Иначе говоря, при k³ n_i

xÎE(|f_k – f|³ s_i ),

так что

|f_k (x) – f(x)| <s_i (k³ n_i )

и тем более

|f_k (x) – f(x)| < e (k³ n_i ).

Теорема доказана, ибо n_i зависит только от e, но не от x.

Структура измеримых функций

При изучении какой-нибудь функции сам собою встает вопрос о точном или приближенном представлении ее с помощью функций более простой природы.

Таковы, например, алгебраические вопросы о разложении многочлена на множители или рациональные дроби на простейшие. Таков же вопрос о разложении непрерывной функции в степенной или тригонометрический ряд и т.п.

В этой части мы устанавливаем различные теоремы о приближении измеримых функций функциями непрерывными, т.е. решаем сходный вопрос для измеримых функций. Эти теоремы позволяют нам найти основное структурное свойство измеримой функции выражаемой теоремой 4.

Теорема 1. Пусть на множестве Е задана измеримая, почти везде конечная функция f ( x ). Каково бы ни было e > 0, существует измеримая ограниченная функция g ( x ), такая, что mE ( f ¹ g )< e .

Д о к а з а т е л ь с т в о. Положим

А_k = E(|f|>k), Q = E(|f| = + ¥).

По условию, mQ = 0. Ввиду очевидных соотношений

А₁ É А₂ É А₃ É …,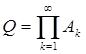

будет (теорема 12) при k®¥

mA_k ®mQ = 0.

Значит, найдется такое k_0, что mA_{k 0} <e.

Определим на множестве E функцию g(x), полагая

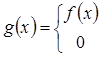
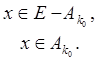
Эта функция измерима и, кроме того, ограничена, поскольку g (x)êk₀ . Наконец, E(f¹g) = A_ko , что и доказывает теорему.

Доказанная теорема означает, что всякая измеримая и почти везде конечная функция становится ограниченной, если пренебречь множеством сколь угодно малой меры.

Определение. Пусть функция F(x) задана на множестве E и x₀ ÎE, причем F(x₀ ) ¹±¥. Говорят, что функция F(x) непрерывна в точке х₀ в двух случаях: 1) если х₀ есть изолированная точка E; 2) если х₀ Î E¢ и соотношения x_n ®x₀ , x_n ÎE влекут соотношение

f(x_n ) ®f(x₀ ).

Если f(x) непрерывна в каждой точке множества E, то говорят, что она непрерывна на этом множестве.

Лемма 1 . Пусть множества F ₁ , F ₂ , …, F_n замкнуты и попарно не пересекаются. Если функция j ( х), заданная на множестве

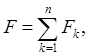
постоянна на каждом из множеств F_{k ,} то она непрерывна на множестве F .

Д о к а з а т е л ь с т в о. Пусть x₀ ÎF’ и x_i ®x₀ , x_i ÎF.

В силу замкнутости множества F точка x₀ принадлежит этому множеству и, стало быть, найдется такое m, что x₀ ÎF_m .