Курсовая работа: Кинематический анализ механизма насоса

V_В =V_A +V_ВA

Скорость точки А известна, скорость относительного вращения точки В вокруг точки А перпендикулярна радиусу вращения отрезку АВ и определяется по формуле:

V_ВА ⁼ ω_ВA ·L_ВA

Скорость точки В направлена вдоль направляющей. Таким образом, получаем векторное уравнение, в котором два вектора известны по направлению, но неизвестны по величине, а третий вектор известен и по величине, и по направлению. Решая это векторное уравнение графическим способом, получим план скоростей для группы Ассура, состоящей из звеньев 2 и 3. В соответствии с векторным уравнением через конец вектора V_A (точку а) проводим направление вектора V_ВА перпендикулярное ВА, а через полюс р -направление вектора V_В , параллельное направляющей. На пересечении этих направлений поставим точку b, а отрезки [аb] и [рb] в масштабе будут представлять скорости V_ВА и V_В . Для определения их величины достаточно на плане измерить соответствующие отрезки и умножить их на масштабный коэффициент μ_v .

V_ВA = [a b]·μ_v = 45 · 0,028 = 1,26 м/с

V_В = [p b] ·μ_v = 0 м/с

Пользуясь построенным планом скоростей, можно определить угловую скорость ω_ВА по формуле:

ω_ВА =V_ВA / L_AВ = 1,26 / 0,52 = 2,42 рад/с

Для определения направления ω_ВА переносим вектор V_ВA в точку В механизма и рассматриваем движение этой точки относительно точки А по направлению скорости V_ВА.

Изложенным выше способом строим планы скоростей для остальных 11 положений.

Результаты построения заносим в таблицу 1.

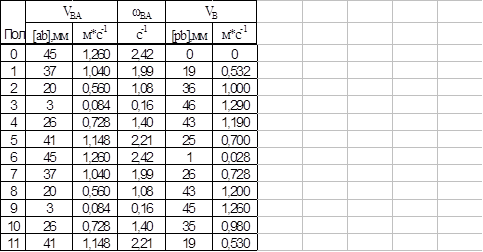
1.2.3 Построение планов ускорений

Определяем ускорение точки А. Так как кривошип по условию движется равномерно (угловое ускорение равно нулю), то ускорение точки А состоит только из нормальной составляющей, которая равна:

а_А = а_А ⁿ =ω² · L_ОА

а_А = 14² · 0,09 = 17,64 м/с²

Вектор а_А направлен по радиусу к центру - от точки А к точке О. Задаемся масштабом плана ускорений μ_а =0,392 м·с^-2 /мм и вычисляем длину отрезка [ра], изображающего в этом масштабе вектор а_А :

[р_а a]= a_A /μ_a = 17,64 / 0,392 = 45 мм

Из произвольной точки р_а , называемой полюсом плана ускорений, в направлении вектора а_А откладываем отрезок [р_а a].

Переходим к группе Ассура звенья 2,3.

Векторное уравнение для точки В группы имеет вид:

ā_В =ā_А +ā_ВА

Ускорение ā_ВA слагается из нормальной и касательной составляющих:

ā_ВA = ā_ВA ⁿ +ā_ВA ^τ

Ускорение ā_ВA ⁿ по величине равно:

ā_ВA ⁿ = ω_ВA ² · L_ВА

ā_ВA ⁿ = 1,99² · 0,52 = 2,06 м/с²

Вычисляем его величину и откладываем в масштабе μ_а от точки а плана ускорений в направлении от точки В к точке А механизма отрезок [an], равный по величине

[an] = а_ВA ⁿ /μ_a = 2,06 / 0,392 = 5,25 мм