Курсовая работа: Комплексные числа в планиметрии

A D A D

Рис. 1 Рис. 2

Решение. Требуется доказать:

Запишем левую часть равенства в комплексной форме: . Воспользовавшись (4a), находим комплексное равенство правой части и непосредственным подсчетом убеждаемся, что она равна левой.

B

P

C

M

N

A

Q D

Рис. 3

Задача 4. Доказать, что сумма квадратов медиан BM , AN , CP треугольника ABC равна суммы квадратов его сторон. (Рис.4 )

Решение. Требуется доказать: Запишем левую часть, воспользовавшись формулами (2) и (4а), и убедимся в том, что она равна правой.

Задача 5. Доказать, что расстояние от вершины С треугольника АВС до точки D, симметричной центру описанной окружности относительно прямой АВ, вычисляется по формуле |CD|² =R² +|AC|² +|BC|² -|AB|² , где R - радиус описанной окружности. (Рис.5 )

Решение. Точка M является серединой АВ, так как центр описанной окружности лежит на пересечении серединных перпендикуляров.

Точка М - середина О D (по условию).

Тогда, 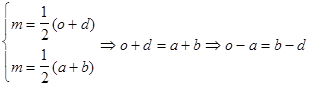. Воспользуемся этим равенством, формулами (2) и (4а) и убедимся в справедливости |CD|² =R² +|AC|² +|BC|² -|AB|² .

D M O

B B

N

P

A

C

A M C