Курсовая работа: Комплексные числа в планиметрии

из которой почленным вычитанием находим:

(17)

В том частном случае, когда хорды АВ и CD перпендикулярны, в силу (15) ab =- cd , и поэтому результат (17) приводится к виду

откуда

(18)

В этом случае точка пересечения определяется только тремя точками A , В, С, так как , и, значит,

(19)

3адача 2. Найти комплексную координату точки пересечения касатель­ных в точках A (а) и B(b) единичной окружности =l. Для искомой координаты z имеем систему

из которой находим:

Поскольку то получаем окончательно:

или (20)

Покажем теперь метод комплексных чисел в действии, применяя его к доказательству классических теорем элементарной геометрии.

Теорема Ньютона . В описанном около окружности четырехуголь­нике середины диагоналей коллинеарны, с центром окружности.

Доказательство. Примем центр окружности за начало, полагая ее радиус равным единице. Обозначим точки касания сторон данного четы­рехугольника A_o B_o C_o D_o через А , В, С, D (в круговом порядке) (рис.4). Пусть М и N — середины диагоналей А_o С_o и B_o D_o соответственно. Тогда согласно (20) точки А_o , В_o , С_o , D_o будут иметь соответственно комплексные координаты:

где a, b, c, d – комплексные координаты точек A, B, C, D.

Поэтому

Вычисляем Поскольку то непосредственно видно, что На основании (6) точки О, М, N коллинеарны.

Теорема Гаусса. Если прямая пересекает прямые, содержащие стороны ВС, СА, АВ треугольника АВС соответственно в точках А₁ , B₁ , C₁ , то середины отрезков АА₁ , ВВ₁ , СС₁ коллинеарны (рис.5).

Доказательство. Используя (11), запишем условия коллинеар­ности троек точек АВ ₁ С, СА ₁ В, ВС ₁ А, A ₁ B ₁ C ₁ :

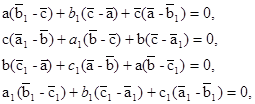(21)

Если М, N , P — середины отрезков AA ₁ , BB ₁ , CC ₁ , то предстоит показать, что

(22)

Так как то доказываемое равенство (22) эквивалентно такому:

или после перемножения:

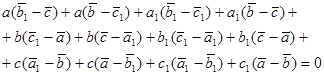(23)

Теперь легко видеть то, что (23) получается почленным сложением ра­венств (21). Доказательство закончено.

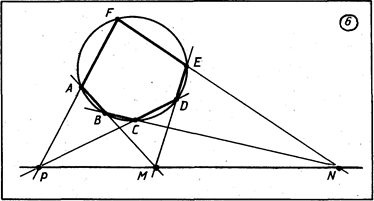
Теорема Паскаля . Точки пересечения прямых, содержащих про­тивоположные стороны вписанного шестиугольника, лежат на одной прямой.

Доказательство. Пусть в окружность вписан шестиугольник ABCDEF и (рис.6). Примем центр окружности за нулевую точку плоскости, а ее радиус - за единицу длины. Тогда согласно (17) имеем:

Вычисляем

ианалогично

Далее находим: