Курсовая работа: Кооперативные игры

но удовлетворяющие условию

0 £ C₁ , C₂ , C₃ £ 1.

Таким образом, классы стратегической эквивалентности общих кооперативных игр трёх игроков могут быть поставлены в соответствие точкам трёхмерного единичного куба подобно тому, как это получилось для игр 4-х игроков с нулевой суммой.

Для игр более 3-х игроков с ненулевой суммой рассмотрения аналогичны.

Для исследования игр большое значение имеет возможность учёта предпочтения дележей, который осуществляется с помощью понятия доминирования.

Определение. Пусть имеется два дележа x = (x₁ , ..., x_n ) и y = (y₁ , ..., y_n ) в кооперативной игре G = {N,u}, и KÌ N – некоторая коалиция. Тогда делёж x доминирует y по коалиции K, если

1) £ u(K) (свойство эффективности доминирующего платежа)

2) x_i > y_i для всех iÎK (свойство предпочтительности)

Свойство эффективности означает, что сравниваемый коалицией делёж x должен быть, реализуемым этой коалицией: сумма выигрышей каждого из членов коалиции не должна превосходить уверенно получаемое ею количество. В противном случае коалиция, встретившись с дележём, дающим ей столько, сколько она самостоятельно не в состоянии добиться, должна согласиться на него и не заниматься его сравнением с какими либо другими дележами.

Условие предпочтительности отражает необходимость “единодушия” в предпочтении со стороны коалиции: если хотя бы одно из неравенств x_i > y_i будет нарушено, т.е. если хотя бы для одного из членов коалиции K выигрыш в условиях дележа y будет не меньшим, чем в условиях дележа x, то можно будет говорить о предпочтении дележа x дележу y не всей коалицией K, а только теми её членами, для которых соответствующее неравенство x_i > y_i соблюдается.

Соотношение доминирования x над y по коалиции K обозначается через

.

Определение. Делёж x доминирует y, если существует такая коалиция K, для которой делёж x доминирует y. Это доминирование обозначается так:

x > y.

Наличие доминирования x > y означает, что в множестве игроков N найдётся коалиция, для которой x предпочтительнее y. Отношение доминирования не обладает полностью свойствами рефлексивности, симметрии, транзитивности, возможна только частичная симметрия и транзитивность. Соотношение доминирования возможно не по всякой коалиции. Так, невозможно доминирование по коалиции, состоящей из одного игрока или из всех игроков.

Справедлива следующая теорема.

Теорема. Если u и u¹ – две стратегически эквивалентные характеристические функции, причём дележам x и y соответствуют дележи и , то из x > y следует >.

Очевидно, все явления, описываемые в терминах доминирования дележей, относятся к классам стратегической эквивалентности, поэтому достаточно изучать эти классы (а не сами игры) для существенных игр по их (0,1)-редуцированной форме, а для несущественных игр – по нулевым играм.

В любой несущественной игре имеется только один делёж, поэтому никаких доминирований в ней нет.

Рассмотрим доминирование дележей в существенной игре на следующем примере.

Пример. Пусть имеется (0,1)-редуцированная форма существенной игры трёх игроков с постоянной суммой (равной 1). Поскольку доминирование невозможно ни по одной из одноэлементных коалиций 1,2,3, а также по коалиции, состоящей из всех трёх игроков, то доминирование возможно только по одной из двухэлементных коалиций {1,2}, {1,3}, {2,3}.

Для наглядности доминирования дележей введём понятие бароцентрических координат. Осями координат служат три оси x₁ , x₂ , x₃ , составляющие между собой одинаковые углы 60^о , ось x₃ находится на расстоянии единицы от точки пересечения осей x₁ и x₂ (рис.1), координаты точки x = (x₁ , x₂ , x₃ ) – соответственно расстояния от этой точки до осей x₁ , x₂ , x₃ , взятые с такими знаками, как указано на рис.1. (Например, для точки x на рис.1. x₁ < 0, x₂ > 0, x₃ > 0).

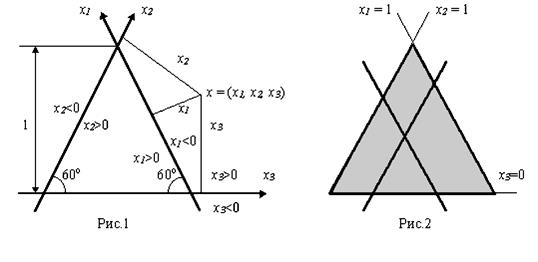
В барицентрической системе координат всегда выполняется равенство

x₁ + x₂ + x₃ = 1.

В плоскости всегда имеется точка с координатами x₁ , x₂ , x₃ , удовлетворяющими равенству (6). По этому бароцентрическая система координат автоматически удовлетворяет одному из условий, определяющих исход игры трёх игроков. С другой стороны, поскольку игра в (0, 1)-редуцированной форме, то точка x должна находиться в заштрихованном треугольнике (см. рис. 2). Дележи x₁ , x₂ , x₃ должны удовлетворять неравенствам

x₁ + x₂ £ u(1, 2), x₁ + x₃ £ u(1, 3), x₂ + x₃ £ u(2, 3).

Очевидно, из условия дополнительности, что

x₁ + x₂ = 1 - x₃ £ 1 = u(1, 2), x₁ + x₃ £ 1, x₂ + x₃ £ 1.