Курсовая работа: Кооперативные игры
К особенностям кооперативных игр относительно существования с-ядра относятся :
1) в несущественной игре с-ядро существует и состоит из единственного дележа этой игры;
2) во всякой существенной игре с постоянной суммой с-ядро пусто.
Для общей игры трёх игроков в (0; 1)-редуцированной форме имеем следующее (рис. 7).
Её характеристическая функция имеет вид :
u(Æ) = u(1) = u(2) = u(3) = 0;
u(1, 2, 3) = 1,
u(1, 2) = С3 ; u(1, 3) = С2 ; u(2, 3) = С1 ,
где 0 £ С1 , С2 , С3 £ 1.
На основании последней теоремы для принадлежности дележа x с-ядру необходимо и достаточно выполнение неравенств
x1 + x2 ³ C3 , x1 + x3 ³ C2 , x2 + x3 ³ C1
или, используя равенство x1 + x2 + x3 = 1, получим
x3 £ 1 - C3 , x2 £ 1 - C2 , x3 £ 1 - C1 . ![]()
3
1 2
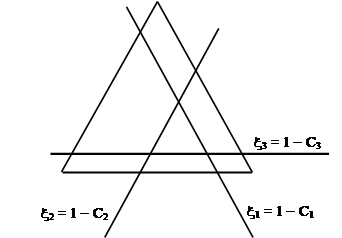
Рис. 7
Это означает, что точка x должна лежать ближе к i-й вершине основного треугольника (см. рис. 7), чем прямая
xi = 1 - Сi (i = 1,2,3) ![]()
Из неравенства (10) путём суммирования получим
x1 + x2 + x3 £ 3 - (С1 + С2 + С3 )
или, учитывая, что x1 + x2 + x3 = 1, получим
С1 + С2 + С3 £ 2. ![]()
Неравенство (12) является необходимым условием существования непустого с-ядра. С другой стороны, если (12) выполняется, то можно взять такие неотрицательные e1 , e2 , e3 , чтобы
![]() ,
,
и положить
xi = 1 - Ci - ei (i = ![]() )
)
Такие значения xi и удовлетворяют неравенствам (10), т.е. такой делёж x = (x1 , x2 , x3 ) принад- лежит с-ядру.
Геометрически непустое с-ядро является заштрихованным треугольником (рис. 7), со сто- ронами, выраженными уравнениями (11)