Курсовая работа: Кооперативные игры

по коалиции {1, 2}, если x₁ > y₁ , x₂ > y₂ ;

по коалиции {1, 3}, если x₁ > y₁ , x₃ > y₃ ;

по коалиции {2, 3}, если x₂ > y₂ , x₃ > y₃ ,

т.е. если делёж y находится в одном из заштрихованных параллелограммов (за исключением трёх граничных прямых, проходящих через точку x) на рис. 3, то делёж x доминирует делёж y, а всякая точка находящаяся в не заштрихованных треугольниках, является предпочтительнее исхода x.

x₃ = - 1 x₂ = - 1

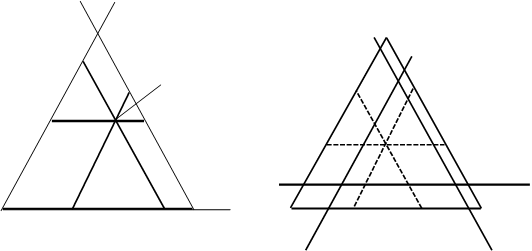x = (x₁ , x₂ , x₃ )

x₃ = 1 - C₃

x₁ = 0

x₁ = 1 - C₁ x₂ = 1 - C₂

Рис.3 Рис. 4

Таким образом, если x и y - два исхода и ни один из них не предпочтительнее другого, то соответствующие точки лежат на прямой, параллельной одной из координатных осей.

Пример. Пусть имеется (0, 1)-редуцированная игра трёх игроков с ненулевой суммой.

Рассмотрим сначала условия доминирования дележа x = (x₁ , x₂ , x₃ ) над дележём y = (y₁ , y₂ , y₃ ) по коалиции {1, 2}. В этом случае имеем :

Поскольку может быть, что C₃ < 1 , то первое из условий (7) нельзя отбросить, как это делает- ся в играх с постоянной суммой. Это значит что, x должна быть не ниже прямой

x₁ + x₂ = C₃ .

Или, учитывая (6), последнее уравнение принимает вид

x₃ = 1 + C₃ .

Таким образом, если делёж x таков, что

x₁ ³ 1 - C₁ , x₂ ³ 1 - C₂ , x₃ ³ 1 - C₃ ,

то имеется три параллелограмма, заштрихованных на рис. 4, находясь в которых, точки x доминируют y.

Если в (8) одно из неравенств, например, третье не имеет места, то есть только 2 парал- лелограмма, заштрихованных на рис. 5, находясь в некоторых точках x доминирует y.

x₁ = 1 - C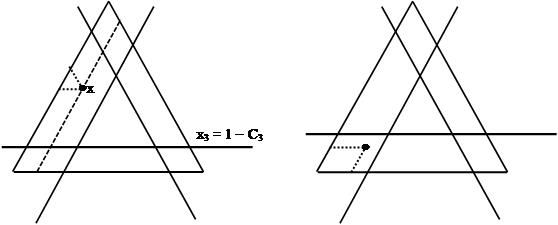₁ x₂ = 1 - C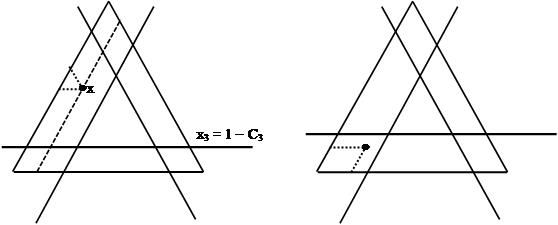₂ x₂ = 1 - C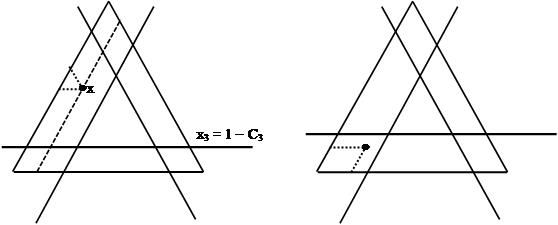₂ x₁ = 1 - C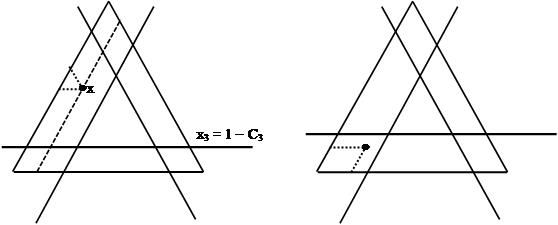₁

x₃ = 1 - C₃

x

Рис. 5 Рис. 6

Из рассмотренного примера видно, что возможно много вариантов, которые возникают при изучении вопросов, связанных с доминированием дележей в кооперативных играх. С ростом числа игроков чрезвычайно быстро растёт количество таких вариантов. В связи с этим возникает необходимость выделения вполне устойчивых дележей, т.е. таких дележей, которые не доминируются никакими другими дележами. Множество вполне устойчивых дележей в кооперативной игре называется с-ядром этой игры.

Теорема. Для того чтобы делёж x принадлежал с-ядру кооперативной игры с характеристической функцией u, необходимо и достаточно, чтобы для любой коалиции K выполнялось неравенство