Курсовая работа: Кооперативные игры

1 2 1 2

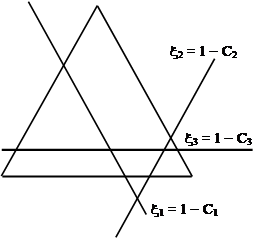
Рис. 8 Рис. 9

при условии, что выполняется соотношение

x₁ + x₂ + x₃ = 1,

и решения любой пары уравнений (11) являются неотрицательными. Так, например, рассмот- рим систему

x₁ = 1 - С₁ , x₂ = 1 - С₂ .

Поскольку 0 £ С₁ £ 1, 0 £ С₂ £ 1, то x₁ , x₂ ³ 0. Отсюда получаем

x₃ = 1 - x₁ - x₂ = 1 - (1 - С₁ ) - (1 - С₂ ) = С₁ + С₂ - 1.

Для того, чтобы было x₃ ³ 0, необходимо чтобы

С₁ + С₂ - 1 ³ 0

или

С₁ + С₂ ³ 1.

В этом случае с-ядро представлено на рис.7 в виде заштрихованного треугольника внутри основного треугольника. Аналогично рассматриваются остальные возможные варианты сочета- ний неравенств. Например, если С₁ + С₂ < 1, то с-ядро имеет вид заштрихованного четырёх- угольника внутри основного треугольника (рис.8). Вообще многогранник, представляющий с‑ядро, образуется как выпуклый многогранник пересечением прямых (11) и строк основного треугольника. Если, например, выполняются неравенства

С₁ + С₂ < 1; С₂ + С₃ < 1; С₁ + С₃ < 1,

то с-ядро представляется в виде шестигранника, заштрихованного на рис.9.

Очевидно, в решение кооперативной игры должны входить дележи, лучшие с определён- ной точки зрения. Так, дележи, входящие в с-ядро, являются устойчивыми в несколько пассив- ном смысле, т.е. при этих обстоятельствах нет оснований отклоняться от такого дележа. Одна- ко, найти делёж, который не только не доминировался бы какими-либо другими дележами, но сам доминировал бы любой другой делёж, не удаётся. Поэтому решение отыскивают на пути расширения класса дележей . И это расширение состоит в том, что решением игры должен быть не один делёж, а некоторое их множество.

Дж. фон Нейман и О. Моргенштерн предложили потребовать от множества дележей, которое принимается в качестве решения кооперативной игры следующие два свойства: внут- реннюю устойчивость, состоящую в том, чтобы дележи из решений нельзя было противопоста- вить друг другу, и внешнюю устойчивость, состоящую в возможности каждому отклонению от решения противопоставлять некоторый делёж, принадлежащий решению. В результате мы приходим к следующему определению.

Определение. Решением по Нейману-Моргенштерну (Н-М-решением) кооперативной игры называется множество R дележей в нём, обладающее следующими свойствами :

1) внутренняя устойчивость: никакие два дележа из R не доминируют друг друга;

2) внешняя устойчивость: каков бы ни был делёж S не принадлежащий R, найдётся делёж r, принадлежащий R, который доминировал бы S.

Содержательная интерпретация Н-М-решения состоит в том, что любые две нормы пове- дения, соответствующие Н-М-решению, не могут быть противопоставлены друг другу; каково бы ни было отклонение от допустимых поведений, найдётся такая коалиция, которая будет стремиться к восстановлению нормы.

Теорема. Если в кооперативной игре существует с-ядро C и Н-М-решение R, то CÌ R.

Свойства Н-М-решений.

Н-М-решение кооперативной игры не может состоять только из одного дележа, т.к. в этом случае характеристическая функция игры несущественная.

Недостатки Н-М-решения.

1. Известны примеры кооперативных игр, которые не имеют Н-М-решений. Более того, в настоящее время не известно каких-либо критериев, позволяющих судить о наличии у кооперативных игр Н-М-решений. Тем самым заложенный в Н-М-решении принцип оптимальности не является универсально реализуемым, и область его реализуемости пока остаётся неопределён- ной.

2. Кооперативные игры, если не имеют Н-М-решения, то, как правило, более одного. Поэтому принцип оптимальности, приводящий к Н-М-решению, не является полным: он, вообще говоря, не в состоянии указать игрокам единственной системы норм распределения выигрыша.