Курсовая работа: Кривые и поверхности второго порядка
I 2 =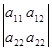
=
= (5 - a)2 – 4 = 6 -2a
I 2 =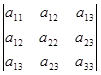
=
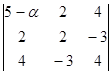= (5 - a)10-24-24-32-9(5 - a)-20 = -a-95
Согласно классификации кривых второго порядка:
I. Если I 2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:
I 2 = 6 - 2a = 0, следовательно, при a = 3 уравнение определяет кривую параболического типа .
При a = 3 I 3 = - a - 95 = -3 - 95 = 98 ¹ 0. Значит, при a = 3 уравнение (3.1) задаёт параболу .
II. Если I 2 ¹ 0, то задаваемая кривая является центральной. Следовательно, при a¹ 3 данное уравнение задаёт центральную кривую.
1. Если I 2 > 0, то уравнение задаёт кривую эллиптического типа:
Значит, при a < 3 уравнение (3.1) задаёт кривую эллиптического типа.
a. Если I 1 I 3 < 0, то уравнение определяет эллипс:
I 1 I 3 = - (7 - a)(a+95) = a2 +88a-665 < 0, при решении получаем aÎ (-95 , 7). Следовательно, при aÎ (-95 , 3)уравнение (3.1) задаёт эллипс .
b. Если I 1 I 3 > 0, то уравнение определяет эллипс:
I 1 I 3 = a2 +88a-665 > 0, при решении получаем aÎ (-¥, -95). Следовательно, при aÎ (-¥ , -95) уравнение (3.1) задаёт мнимый эллипс .
c. Если I 3 = 0, то уравнение определяет две мнимые пересекающиеся прямые:
I 3 = -a - 95 = 0, при решении получаем a - 95. Следовательно, при a = - 95 уравнение (3.1) задаёт две мнимые пересекающиеся прямые .
2. Если I 2 < 0, то уравнение задаёт кривую гиперболического типа:
Значит, при a > 3 уравнение (3.1) задаёт кривую гиперболического типа.
a. Если I 3 ¹ 0, то уравнение определяет гиперболу:
I 3 = -a - 95 ¹ 0, получаем a¹ -95. Следовательно, при aÎ (3 , +¥) уравнение (3.1) задаёт гиперболу .
Согласно полученным данным, построим таблицу:
| aÎ(-¥ , -95) | a = -95 | aÎ(-95 , 3) | a = 3 | aÎ(3 , +¥) |
| Мнимый эллипс | Две мнимые пересекающиеся прямые | Эллипс | Парабола | Гипербола |
2. Приведение к каноническому виду
При a = 0 уравнение (3.1) принимает вид:
5x2 + 4xy + 2y2 + 8x - 6y + 5 = 0 (3.2)
Приведем уравнение кривой (3.2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.
a) Характеристическое уравнения для данной кривой будет иметь вид:
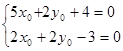
A(x, y) = 5x2 + 4xy + 2y2
Откуда следует, корни характеристического уравнения есть: l1 = 1, l2 = 6.
Расположение эллипса относительно начальной системы координат будет известно, если мы будем знать координаты центра и угловой коэффициент вещественной оси эллипса.