Курсовая работа: Кривые и поверхности второго порядка
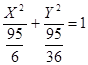 (3.6)
(3.6)
- это каноническое уравнение данной кривой (3.1) при a = 0.
3. Построение графиков
Подтвердим результаты проведённого исследования данного уравнения кривой (3.1) второго порядка, построив соответствующие графики кривых при разных a.
При a = 3 уравнение (3.1) принимает вид:
2x2 + 4xy + 3y2 + 8x – 6y +5 = 0
Графиком данного уравнения является парабола:
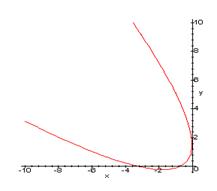
При a = 6 уравнение (3.1) принимает вид:
x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является гипербола:
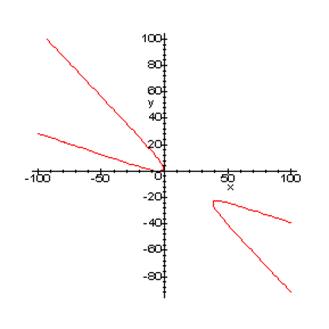
При a = 0 уравнение (3.1) принимает вид
5x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0
Графиком данного уравнения является эллипс. Изобразим в данной системе также график канонического уравнения эллипса (3.6):
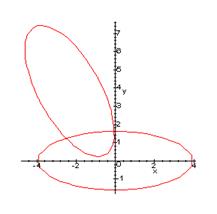
4. Вывод
Исследовав данное общее уравнение кривой второго порядка, мы установили, что при значении параметра a = 0 уравнение задаёт эллипс . Привели уравнение к каноническому виду, применяя преобразования параллельного переноса и поворота. При параллельном переносе коэффициенты при первых степенях стали равны нулю, при повороте координатных осей коэффициенты при смешанном произведении стали равны нулю. Построили графики для всех фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат.
Часть II. Исследование поверхности второго порядка
1. Определение типа поверхности
Для данного уравнения поверхности второго порядка:
4x2 - z2 + 12xz + 6y - 8z + 5 = 0 (4.1)
Определить тип поверхности с помощью инвариантов.
![]() 4 + 0 -1 = 3
4 + 0 -1 = 3
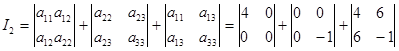 = - 4 – 36 = - 40
= - 4 – 36 = - 40
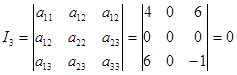
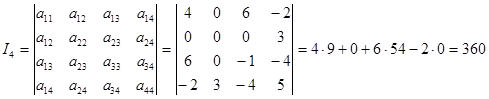
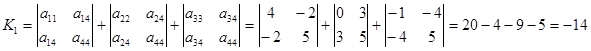

Определим характер расположения центра: Данная поверхность не имеет центра , так как выполняется условие I 3 = 0, I 4 ¹ 0. При этом инвариант I 4 = 360 > 0, следовательно, графиком уравнения (4.1) является гиперболический параболоид .
2. Приведение к каноническому виду
Совершим параллельный перенос начала координат в некоторую точку O '( x 0 , y 0 , z 0 ) . При этом координаты x , y , z произвольной точки пространства в системе координат Oxyz и координаты x ', y ', z ' этой же точки в новой системе координат в системе координат O ' x ' y ' z ' связаны соотношением: