Курсовая работа: Кривые и поверхности второго порядка

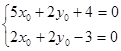
Откуда мы находим x₀ = - и y₀ = . Следовательно, точка O ¢ (-,) есть центр данной кривой.

Угловой коэффициент оси O ¢X можем определить по формуле:

б) Совершим параллельный перенос начала координат в точкуO ¢ (x₀ , y₀ ). При этом координаты x, yпроизвольной точки плоскости в системе координат xOy и координаты x ', y ' в новой системе координат x 'O 'y ' связаны соотношениями:

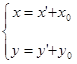
Подставив данные выражения в уравнение (3.1), получим:

5(x₀ + x¢)² + 4(x₀ + x¢)(y₀ + y¢) + 2(y₀ + y¢)² + 8(x₀ + x¢) - 6(y₀ + y¢) + 5=0

Раскрыв скобки и приведя подобные члены, получим:

5x¢² +4x¢y¢+2y¢² +(10x₀ +4x₀ + 8)x¢ + (4x₀ + 4y₀ - 6)y¢ + (5x₀ ² + 4x₀ y₀ + 2y₀ ² + 8x₀ - 6y₀ + 5) = 0 (3.3)

В данном уравнении коэффициенты при x¢ и y¢ приравняем к нулю и получим систему уравнений:

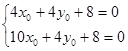
Решив эту систему уравнений, мы получим, найденные уже раннее, координаты центра O ¢ , x₀ = - и y₀ = . Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x 'O 'y ' :

5x¢² + 4x¢y¢ + 2y¢² + () = 0

5x¢² + 4x¢y¢ + 2y¢² - = 0 (3.4)

в) Так как a₁₂ = 2 ¹ 0, то для дальнейшего упрощения необходимо произвести поворота осей координат на угол a . При повороте осей координат на уголa координаты x', y' произвольной точки М плоскости в системе координат x 'O 'y ' и координаты X, Y в новой системе координат XO'Y связаны соотношениями:

Подставим данные выражения в уравнение (3.4), получим:

5(Xcosa - Ysina)² + 4(Xcosa - Ysina)(Xsina + Ycosa) + 2(Xsina + Ycosa)² - = 0

(5cos² a + 4sinacosa + 2sin² a)X² + (-6sinacosa + 4cos² a - 4sin² a)XY +

(5sin² a - 4sinacosa + 2cos² a)Y² - = 0 (3.5)

В полученном выражении найдём такой угол a, чтобы коэффициент при XY стал равен нулю, для этого необходимо:

-6sinacosa + 4cos² a - 4sin² a = 0

2tg² a + 3tga - 2=0

Откуда, при решении, находим два значения tga = -2 и tga = .

В первом задании мы нашли, что угловой коэффициент вещественной оси O ' X эллипса равен k = -2. Так как угловой коэффициент равен тангенсу, то из двух найдённых значений выберем tga = -2. Следовательно:

cosa = , sina =

Подставив данные значения для sina и cosa в уравнение (3.5), коэффициент при XY станет равным нулю, получим:

()X² + ()Y² - = 0