Курсовая работа: Кривые и поверхности второго порядка
Подставляя уравнения (4.2) в уравнение (4.1) получим уравнение поверхности S в новой системе координат O ' x ' y ' z ' :
4(x'+x0 )2 - (z'+z0 )2 + 12(x'+x0 )(z'+z0 ) + 6y' - 8(z'+z0 ) + 5 = 0
4x'2 + 8x'x0 + 4x0 2 - z'2 - 2z'z0 - z0 2 + 12x'z' + 12z'z0 + 12x0 z' + 12x0 z0 + 6y' - 8z' - 8z0 + 5 = 0
4x'2 - z'2 + 12x'z' + 6y' + (12x0 - 2z0 - 8)z' + (8x0 + 12z0 )x' + (4x0 2 - z0 2 + 12x0 z0 - 8z0 +5)=0 (4.3)
Для того, чтобы новое начало координат O'(x0 , y0 , z0 ) было центром поверхности (4.1) необходимо и достаточно, чтобы в уравнении (4.3) отсутствовал член с x' и z' в первой степени:
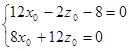
Решая данную систему, находим x0 = 
и y0 = 
. Подставим полученные значения в уравнение (4.2):
4x'2 - z'2 + 12x'z' + 6y' + (
)z' + (
)x' + (
) = 0
4x'2 - z'2 + 12x'z' + 6y' + 
=0 (4.4)
Поскольку коэффициент при x'z' не равен нулю, то продолжим дальнейшее преобразование, совершив поворот осей координат на угол a. Координаты произвольной точки поверхности будут связаны следующими соотношениями:
(4.5)
Подставив выражения из (4.5) в уравнение (4.4), получим следующее:
4(Xcosa - Zsina)2 – (Xsina + Zcosa)2 + 12(Xcosa - Zsina)(Xsina + Zcosa) + 6Y + = 0
4X2 cos2 a - 8XZcosasina + 4Z2sin2 a - X2sin2 a - 2XZsin2 a - 2XZcosasina -Z2 cos2 a + 12X2 cosasina + 12XZcos2 a - 12XZsin2 a - 12Z2 sinacosa + 6Y + = 0
(4cos2 a-sin2 a+12cosasina)X2 +(4sin2 a-cos2 a-12sinacosa)+(-8cosasina-2cosasina+12cos2 a-12sin2 a)XZ+6Y+=0 (4.6)
Найдём угол a такой, что коэффициент при XZ будет равен нулю:
-8cosasina-2cosasina+12cos2 a-12sin2 a=0
6tg2 a+5tga-6=0
D = 25+144 = 169 = 132
Откуда следует, что tga = 
или tga = 
. Возьмём tga = . Тогда найдём cosa=
=
, sina=
. Подставим найдённые значения в уравнение (4.6):
(
)X2 +(
)Z2 +(
)XZ+6Y+=0
(4.7)
- это каноническое уравнение поверхности (4.1). Оно имеет сдвиг по оси O'Y на (-
).
3. Исследование формы поверхности методом сечений
Проведём исследование графика уравнения (4.7) методом сечения плоскостями.
Рассмотрим линии 
, полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:
Следовательно, уравнения проекций линий на плоскость ZO ' X имеют вид:
:
Рассмотрим три случая: