Курсовая работа: Линейные электрические цепи постоянного и синусоидального тока

I6 = J1-I11 = -1 A

I5 = I22 + J1 = 2 A

Проверка

1) Баллансмощностей:

E5*I5 + E6*I6 +J2*(U2+I2*R2) = I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4+I5^2*R5+I1^2*R7

40 Вт = 40 Вт.

2) Проверка по первому закону Киргофа:

I1 = I5 + I3;

I1 = I2 + I4;

I4 = I5 + I6;

I2 + I6 = I3;

Задание 2

Принципиальная схема цепи выглядит следующим образом:

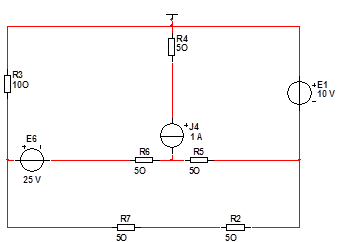
Найдем количество уравнений. Так как в цепи присутствуют независимые источники тока, то мы имеем:

Теперь выберем независимые контуры. Пусть первый контур состоит из ветвей 1 и 2, и по нему течет ток I11 против часовой стрелки. Пусть второй контур состоит из ветвей 1 и 3, по нему течет ток I22 против часовой стрелки.

Запишем систему уравнений по методу контурных токов, учитывая J1:

(R3 + R6 +R5) * I11 – (R5 + R6) * I22 = – (R3 + R6) * J1 – E6 + E1

– (R5 + R6) * I11 + (R2 + R5 + R6 + R7) * I22 = R6 * J1 + E6

20 * I11 – 10 * I22 = -30

-10 * I11 + 20 * I22 = 30

Решим систему по методу Крамера. Найдем определители:

D = 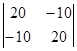= 300, D11 = 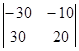= -300, D22 = 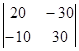= 300.

Найдем контурные токи:

I11 = D11/D = -1 A; I22 = D22/D = 1 A

Токи в ветвях найдем как сумму контурных токов, текущих по ним, с учетом знаков:

I2 = I7 = I22 = 1A