Курсовая работа: Линейные электрические цепи постоянного и синусоидального тока
Задания
Цель работы: Расчёт и исследование цепей постоянного и синусоидального тока.
Определить:
1) токи всех ветвей схемы, используя МКТ, МУП.
2) ток в выделенной ветви, используя МЭГi, МЭГu.
3) проверить баланс мощностей
4) привести схемы в EWB или Ms для измерения токов ветвей, напряжений на элементах.
Задание 1

Дано:
R1 = 3 Ом, R2 = 10 Ом, R4 = 10 Ом, R5 = 5 Ом, R7 = 2 Ом,
J2 = 1A, E5 = 20B, E6 = 5B.
Задание 2

Дано:
R2 = 5 Ом, R3 = 10 Ом, R4 = 5 Ом, R5 = 5 Ом, R6 = 5 Ом, R7 = 5 Ом,
J4 = 1 A, E1 = 10 B, E6 = 25 B.
Задача 3

Дано:
R1 = 6 Ом, R2 = 3 Ом, R4 = 10 Ом, R5 = 1 Ом, R6 = 3 Ом, R7 = 3 Ом, R8 = 6 Ом,
J2 = 1 A, E3 = 12 B, E4 = 24 B.
Задание 4

Дано:
R1 = 220 Ом, R2 = 120 Ом, R3 = 150 Ом, R4 = 200 Ом, E1 = 10B, E3 = 15B,
f = 120МГц, C1 = 253 мкФ, C2 = 345 мкФ, L1 = 276 мГн, L2 = 138 мГн.
Линейные электрические цепи постоянного тока
Теория, метод контурных токов
Нам дана линейная электрическая цепь. Задача, заключается в нахождении сначала контурных токов, затем и токов в ветвях. Сначала выбираем произвольно направления токов в контурах, его можно выбрать по часовой стрелке и против часовой стрелки, но это условно, так как исходя из полученного в дальнейшем знака, мы будем судить о направлении тока. Воспользуемся фундаментальными законами Кирхгофа. В частности первый закон Кирхгофа: алгебраическая сумма токов, подтекающих к любому узлу схемы, равна 0. Применив закон к примеру (рис. 1) получаем систему уравнений:
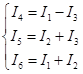 .
.
Выбираем дерево, которое включает в себя максимальное количество ветвей без источников тока. Пусть это будут ветви, содержащие ![]() . Затем выбираем контура, и выбираем обход контура. Воспользуемся вторым законом Кирхгофа: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура. Для выбранных нами контуров составляем систему уравнений Кирхгофа:
. Затем выбираем контура, и выбираем обход контура. Воспользуемся вторым законом Кирхгофа: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура. Для выбранных нами контуров составляем систему уравнений Кирхгофа:
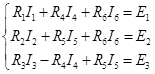
Возьмем токи из первого закона Кирхгофа и подставим их в уравнения из второго закона Кирхгофа. Получим:
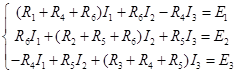
--> ЧИТАТЬ ПОЛНОСТЬЮ <--