Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления
и является квадратичной функцией от начальных значений отклонения вектора состояния.
Таким образом, получаем, что при 
оптимальное управление приобретает форму стационарной обратной связи по состоянию
где 
— решение алгебраического матричного уравнения Риккати.
5.1.1. Решение алгебраического уравнения Риккати методом диагонализации
Для решения данной задачи найдем весовые матрицы 
и 
:
Выберем произвольно 
, тогда
Взяв значения 
из решения задачи L – проблемы моментов получим:
Матрицы системы имеют вид:
, 
.
Введем расширенный вектор состояния 
.
Тогда матрица Z будет иметь следующий вид: 
,
или в численном виде
.
Собственные значения матрицы 
: 
.
Зная собственные значения и собственные вектора матрицы Z , построим матрицу 
По определению все решения должны быть устойчивы при любых начальных условиях 
, т.е. при 
. Чтобы не оперировать комплексными числами, осуществим следующий переход. Пусть:
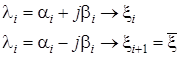
Тогда матрица формируется следующим образом:
.
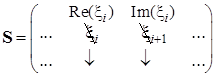Можно показать, что матрицу можно получить из прямой матрицы собственных векторов:
,
.
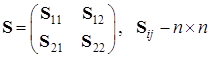Установившееся решение уравнения Риккати, полученное с помощью скрипта Solve_Riccati_Method_Diag.m. имеет вид:
