Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления

.

3.2 Оптимальная L – проблема моментов в пространстве состояний

Система задана в виде:

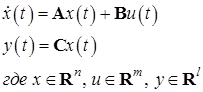
Решение ДУ имеет вид:

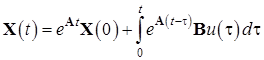, при имеем:

.

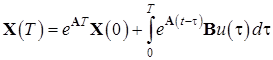Составим моментные уравнения:

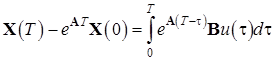
Подставляя необходимые данные в выше приведенные формулы, получим следующие моменты и моментные функции:

Числовое значение найденных моментов:

Моментные функции:

Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).

Из этого следует, что функционал, значения , управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).

Оптимальное управление имеет вид:

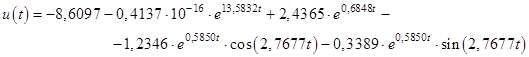
Проверим правильность полученного решения.

Эталонные значения координат в начальный и конечный момент времени:

,

,

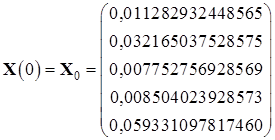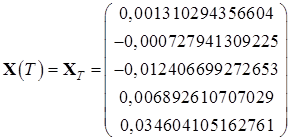
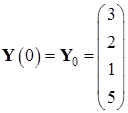Найденные значения координат в начальный и конечный момент времени:

,

,

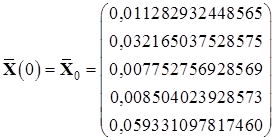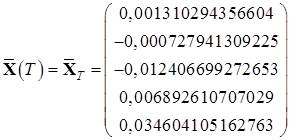
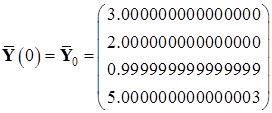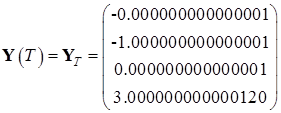
Вычислим погрешность полученных результатов:

,
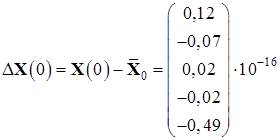