Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления
Формируем целевую функцию (по второму методу выбора начального допустимого базиса)
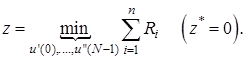(14)
б) Решение задачи быстродействия
Предположим, что 
, где 
– оптимальное число шагов. Так как значение 
нам неизвестно (но 
известно точно), выбираем некоторое начальное 
и решаем задачу линейного программирования (12)-(14).
При этом
Общее число столбцов в симплекс-таблице: 
Число базисных переменных: 
Сформируем 
строку. Имеем
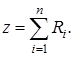
Выразим из уравнения (12) начальные базисные переменные 
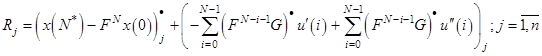
и подставим в целевую функцию. Получим 
– строку
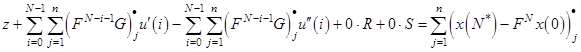(15)
Решаем задачу (12) – (14) симплекс-методом.
В случае,
если 
, 
– малое число 
иначе
1) если 
увеличить 
и целое,рвернуться к первому шагу формирования задачи линейного программирования;
2) если 
(не все управления будут равны предельным, могут быть, в том числе нулевые)), 
, уменьшить 
, вернуться к первому шагу формирования задачи линейного программирования.
Решения данной задачи получено с помощью пакета Matlab 7.4 (скрипт SimplexMetod2.m): 
Рис. 14 . График фазовой координаты 
.
Рис. 15 . График фазовой координаты 
.
Рис. 16 . График 
.
Рис. 17 . График оптимального управления 
.