Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления
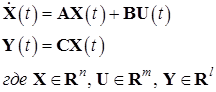
Переходя в область изображений описание системы в пространстве состояний будет иметь следующий вид:
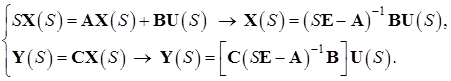
1.2.1 Матрица Фробениуса
Получим выражения, которые определяют вектор состояний и выход заданного объекта в общем виде:
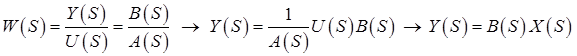 .
.
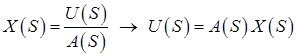 .
.
Тогда получим:
![]() (1)
(1)
![]() (2)
(2)
Числитель передаточной функции имеет вид: ![]() .
.
Знаменатель передаточной функции:
![]() .
.
Тогда согласно равенству (1) и (2) имеем
![]() ,
,
![]() .
.
Перейдем из области изображений в область оригиналов
![]() ,
,
![]()
и затем перейдем к нормальной форме Коши
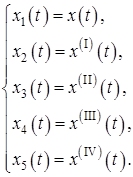
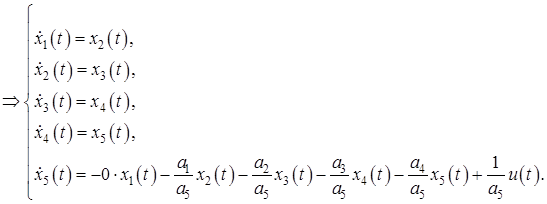
![]() .
.
Запишем матрицы состояний
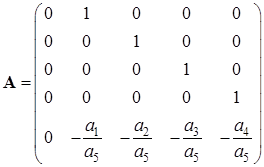 ,
,  ,
, ![]()
Численное значение матриц состояний:
 ,
,  ,
,
![]()
1.2.2 Метод параллельной декомпозиции
Запишем передаточную функцию объекта в другом виде, а именно: