Курсовая работа: Математическая модель в пространстве состояний линейного стационарного объекта управления
Закон оптимального управления в данной задаче имеет вид
![]()
Матричное дифференциальное уравнение Риккати будет иметь следующий вид:
![]()
Если обозначить ![]() то можно записать
то можно записать
![]()
Уравнение замкнутой скорректированной системы примет вид
![]()
Матрицы ![]() заданы в пункте 5.1.1.
заданы в пункте 5.1.1.
Весовые матрицы ![]() и
и ![]() имеют следующий вид:
имеют следующий вид:
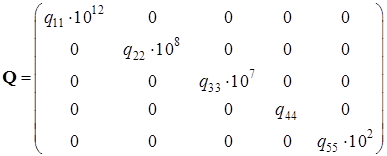 ,
, ![]() .
.
Используя скрипт AKOR_stabilizaciya_na_konech_interval.m получили следующие результаты:
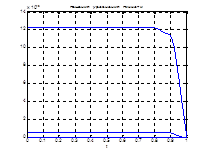
Рис.26. Графики решения уравнения Риккати.
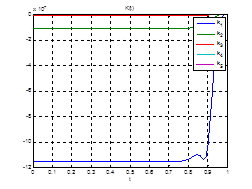
Рис.27. Графики коэффициентов регулятора обратной связи.
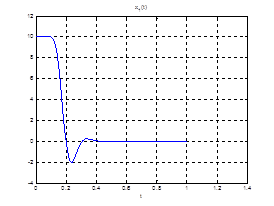
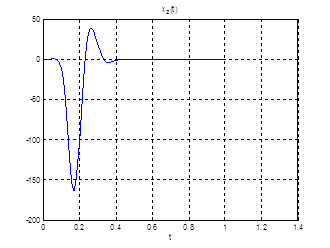
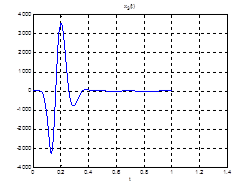
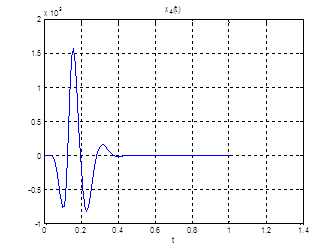
Рис.28. Графики фазовых координат.
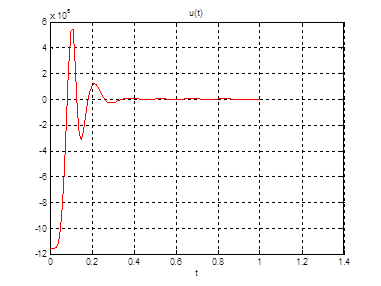
Рис.29. График управления.
Сравним, как стабилизируется система управления с постоянными и переменными коэффициентами регулятора обратной связи на начальном этапе:
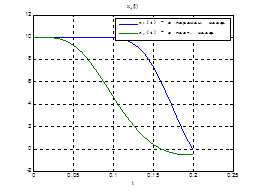
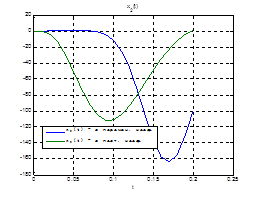
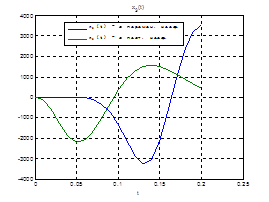
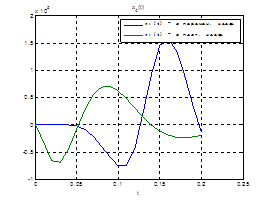
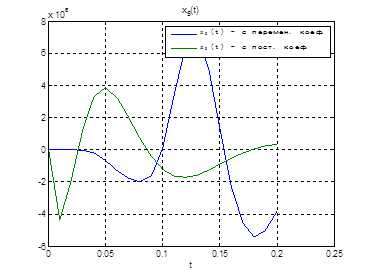
Рис.30. Графики фазовых координат.
Выводы: из графиков видно, что система, у которой коэффициенты регулятора меняются со временем, стабилизируется не хуже, чем, система, у которой коэффициенты регулятора не изменяются.
5.3 Задача АКОР – стабилизации для компенсации
известного возмущающего воздействия
Рассмотрим систему вида
![]() ,
,