Курсовая работа: Метод ортогонализации и метод сопряженных градиентов
Метод можно обобщить. Пусть каким-то образом удалось найти систему 2n векторов ![]() так, что
так, что
![]() =0 при
=0 при ![]() . (12)
. (12)
Умножая обе части равенства (1) на ![]() и используя представление
и используя представление ![]() через
через ![]() , как и ранее, получим:
, как и ранее, получим:
![]() . (13)
. (13)
Опять получилась система линейных алгебраических уравнений с треугольной матрицей для определения ![]() . Несколько усложнив вычисления можно получить систему диагонального вида. Для этого построим три системы векторов
. Несколько усложнив вычисления можно получить систему диагонального вида. Для этого построим три системы векторов ![]() , так что имеют место равенства:
, так что имеют место равенства:
![]() (14)
(14)
![]() (15)
(15)
![]()
![]() (16)
(16)
Тогда
![]() , (17)
, (17)
так как при i<r
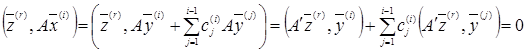 (18)
(18)
и при i>r
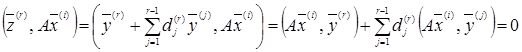 (19)
(19)
Таким образом,
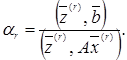 (20)
(20)
Остановимся подробнее на первом из описанных методов. Рассмотрим случай, когда матрица А симметрическая и положительно определенная. Последнее означает, что для любого вектора ![]() квадратичная форма его компонент
квадратичная форма его компонент ![]() больше или равна нулю, причем равенство нулю возможно в том и только том случае, если вектор
больше или равна нулю, причем равенство нулю возможно в том и только том случае, если вектор ![]() нулевой. Как мы видели ранее, нужно построить систему векторов
нулевой. Как мы видели ранее, нужно построить систему векторов ![]() , удовлетворяющих условиям
, удовлетворяющих условиям
![]() =0
=0 ![]() . (21)
. (21)
Это построение можно осуществить следующим образом. Исходим из какой-то системы линейно независимых векторов ![]() , например из системы единичных векторов, направленных по координатным осям:
, например из системы единичных векторов, направленных по координатным осям:
 (22)
(22)
Далее проводим «ортогонализацию». Принимаем ![]() и ищем
и ищем ![]() в виде
в виде
![]() . (23)
. (23)
Из условия ![]() находим:
находим:
 (24)
(24)
Ищем ![]() в виде
в виде
![]() . (25)
. (25)
Условия ![]() влекут за собой
влекут за собой

 (26)
(26)
Далее поступаем также.
Процесс будет осуществим, так как все ![]() . Это же обеспечит нам разрешимость системы для определения коэффициентов
. Это же обеспечит нам разрешимость системы для определения коэффициентов ![]() . Заметим, что в нашем случае это будет процесс настоящей ортогонализации, если в пространстве векторов ввести новое скалярное произведение при помощи соотношения
. Заметим, что в нашем случае это будет процесс настоящей ортогонализации, если в пространстве векторов ввести новое скалярное произведение при помощи соотношения