Курсовая работа: Метод ортогонализации и метод сопряженных градиентов

(7)

и через обозначим новую невязку системы

. (8)

Вектор направлен по нормали к поверхности в точке , а вектор параллелен касательной плоскости в этой точке. Поэтому

. (9)

Гиперплоскость (7) проходит через точку , так как

.

При любом вектор параллелен некоторой нормальной плоскости к поверхности в точке . Найдем среди них тот, который лежит в гиперплоскости (7), т.е. ортогонален к . Из условия ортогональности имеем:

,

или

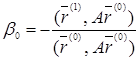. (10)

Вектор

(11)

имеет направление нормали к сечению поверхности гиперплоскости (7) в точке . Будем двигаться из точки в направлении вектора до тех пор, пока функция достигнет минимума. Это будет при

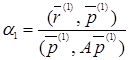. (12)

Вектор

примем за новое приближение к решению системы. Вектор невязок

(13)

имеет направление нормали к поверхности в точке . Покажем, что он будет ортогонален к и . В самом деле, используя (9), (11), (12), (13), имеем:

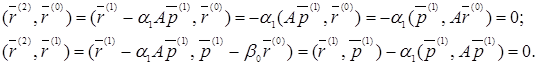
Рассмотрим гиперплоскость (n-2) – х измерений

, (14)

проходящую через точку . Эта гиперплоскость содержит и , так как мы ранее видели, что , а

.

Вектор при любом параллелен гиперплоскости (7), так как

.

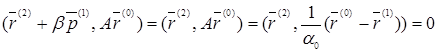Подберем так, чтобы он был параллелен и гиперплоскости (14), т.е. потребуем ортогональности к вектору . Будем иметь:

,