Курсовая работа: Метод ортогонализации и метод сопряженных градиентов

где

(40)

Процесс будет осуществим, если система уравнений линейно независима. В результате мы придем к новой системе , где матрица С будет ортогональной, т.е. обладает свойством СС¢=I.

Таким образом, решение системы можно записать в виде

. (41)

Практически, вследствие ошибок округления, СС¢ будет отлична от единичной матрицы и может оказаться целесообразным произвести несколько итераций для системы .

2. Метод сопряженных градиентов

2.1 Первый алгоритм метода

Пусть требуется решить систему линейных алгебраических уравнений

(1)

с положительно определенной матрицей A порядка n.

Рассмотрим функционал

, (2)

представляющий многочлен второго порядка относительно x₁ , x₂ , …, x_n . Обозначим через решение системы (1), т.е. . В силу симметричности и положительной определенности матрицы, имеем:

При этом знак равенства возможен лишь при . Таким образом, задача решения уравнения (1) сводится к задаче отыскания вектора , обращающего в минимум функционал (2).

Для отыскания такого вектора применим следующий метод.

Пусть – произвольный начальный вектор, а

(4)

– вектор невязок системы. Покажем, что вектор невязок имеет направление нормали к поверхности в точке . В самом деле, направление нормали совпадает с направлением быстрейшего изменения функции в точке . Это направление мы найдем, если найдем среди векторов , для которых , такой вектор, что

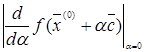
имеет наибольшее значение. Но

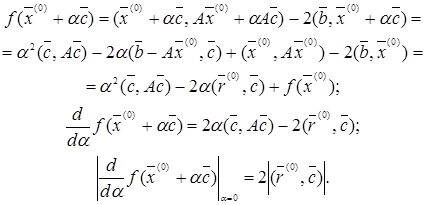
Но среди векторов постоянный длины достигает максимального значения, если имеет направление вектора или ему противоположное. Утверждение доказано. Будем двигаться из точки в направлении вектора до тех пор, пока функция достигает минимального значения. Это будет при , т.е. при

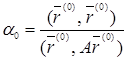. (5)

Вектор

(6)

и принимаем за новое приближение к решению.