1. Сформулируйте 1 признак равенства треугольников.

2. Сформулируйте 2 признак равенства треугольников.

3. Какой треугольник называется равнобедренным?

4. Сформулируйте признак равнобедренного треугольника.

5. Сформулируйте свойства равнобедренного треугольника.

6. Чем отличается признак геометрической фигуры от ее свойства?

7. Сформулируйте 3 признак равенства треугольников.

8. Какой треугольник называется равносторонним?

9. Что считается признаком, что – свойством равностороннего D-ка?

10. К каждой ли теореме существует обратная?

11. Приведите пример теоремы, к которой не существует обратной.

12. Приведите пример теоремы, к которой существует обратная.

13. Как строится обратная теорема?

14. Сформулируйте признаки равенства прямоугольных треугольников.

После фронтального опроса учитель проводит беседу по опорным конспектам на доске. Если необходимо, то ученики класса дополняют и исправляют записи на доске.

ІІ. Решение задач.

Два ученика около доски решают задачи по готовым рисункам, которые выполнены учителем до урока. Если необходимо, то ученики класса дополняют и исправляют записи на доске.

Задачи по готовым рисункам

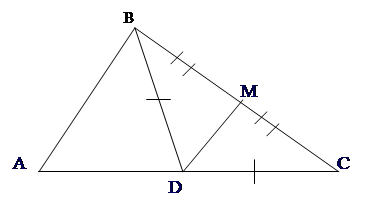1. ????: D???, BD=CD, BM=CM, ÐDBM=40⁰ ,ÐADB=80⁰ . ?????: ÐBDM, ÐMDC, ÐDMC, ÐMCD.

Ответ: ÐBDM=ÐMDC=50⁰ , ÐDMC=90⁰ , ÐMCD=40⁰ .

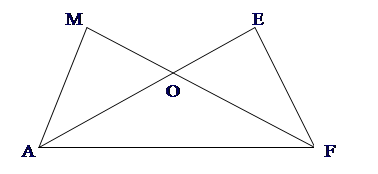
2. DAOM=DFOE, периметр DOEF=40 см , AF=20 см. Найти: периметр DAEF.

Ответ: 60 см.

III. Физкультурная пауза

(Ученики повторяют за учителем все движения.)

IV. Устная работа.

Учитель с учениками устно решает задачи по готовым рисункам, изображенным на плакатах. Ученики должны найти на рисунках равные треугольники и объяснить равенство, назвав соответственный признак равенства треугольников.

Задачи для устного решения.

ІV. Домашнее задание.

УРОК 5

Тема урока: “Решение прикладных задач»

Цель урока:

• рассмотреть жизненные и прикладные задачи, на которых можно продемонстрировать важную роль признаков равенства треугольников в жизни, научить учеников творчески применять признаки равенства треугольников во время решения задач.

Ход урока

І. Гимнастика ума.

При написании математического диктанта повторяются три признака равенства треугольников, понятие равнобедренного треугольника, его свойства и признаки. Цель диктанта – систематизировать и повторить важные факты данной темы, способствовать развитию внимания, логического мышления и математического зрения учеников, сформировать навыки умственной деятельности. Учитель зачитывает задания, а ученики записывают ответы к ним или ставят знак «+», если учитель называет правильный ответ.

После выполнения задания ученики обмениваются тетрадями для перекрес-тной проверки. Такая система контроля развивает у учеников честность и объективность в оценивании результатов своей деятельности и деятельности одноклассников. Задание диктанта предлагается по вариантам.

Математический диктант.

Вариант І.

1. В DKNO и DPQT равные стороны KN и PQ и углы K и P. Какое еще равенство должно выполняться, чтобы треугольники были равны по 1 признаку равенства треугольников?

2. У равных DBCD и DMPQ углы B и D равны соответственно углам M и Q. Что следует из условия по 2-му признаку равенства треугольников?

3. В DАВС проведены медианы AD, BE, CF. Длины отрезков AF, AE, BD соответственно равны 3 см, 5 см, 6 см. Найти периметр DАВС.

4. В DАВС и DPOT стороны AB=PO, BC=OT. Какое еще условие должно выполняться, чтобы треугольники были равны по 3 признаку равенства треугольников?

5. Продолжить предложение: “В равнобедренном треугольнике медиана является ...”

Вариант ІІ.

1. В DABC и DDEF равные стороны AB и DE и углы A и D. Какое еще равенство должно выполняться, чтобы треугольники были равными по 1 признаку равенства треугольников?

2. У равных DMRQ и DKLT углы M и Q равны соответственно углам K и T. Что следует из условия согласно 2 признаку равенства треугольников?

3. В DАВС проведены биссектрисы AD, BE, CF. Градусные меры углов соответственно равны ÐBAD=30, ÐCBE=40, ÐACE=20. найдите сумму углов DАВС.

4. В DMNQ и DRST стороны MN=RT, NQ=NS. Какое еще условие должно выполняться, чтобы треугольники были равны по 3 признаку равенства треугольников?

5. Продолжить предложение: “Если в треугольнике все углы равны, то он ...”

Ответы учителя.

І вариант. 1. KO=PT. 2. BD¹MQ. 3. 28 см. 4. AC=PT. 5. биссектрисой и высотой

IІ вариант. 1. AC=DF. 2. MQ¹KT. 3. 180⁰ . 4. MQ=RS. 5. равносторонний

ІІ. Решение прикладных задач.

Задача 1. Чтобы измерить на местности расстояние между двумя точками А и В, между которыми нельзя пройти с мерной цепью , выбирают такую точку С, из которой были бы видны как точка А, так и В и из которой можно было бы к ним пройти. Провешивают*) АС и ВС, продолжают их за точку С и отмеряют CD = AC и EC = CB. Тогда отрезок ED равен искомому расстоянию АВ. Почему?

*) То есть отмечают направление шестами - вехами.

Задача 2 . Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ и на его продолжении отмеряют произвольный отрезок BE. Выбирают на местности точку D, из которой можно было бы видеть точку А и пройти к точкам В и E. Провешивают прямые BDG и EDF и отмеряют FD = DE и DG = BD. Затем идут по прямой FG, смотря на точку А, пока не найдут такую точку Н, которая лежит на прямой AD. Тогда НG равно искомому расстоянию. Доказать.

Задача 3. Чтобы измерить расстояние между пунктами А и В, расположенными на разных берегах реки, при помощи эккера провешивают перпендикулярно к АВ отрезок BD произвольной длины. Делят BD в точке Е пополам. Проводят перпендикуляр DC к BD в точке D; идут по DC, смотря на А, до точки С, которая лежит на прямой АЕ. Длина DC равна АВ. Доказать.

ІII. Домашнее задание.

Задача 1. На каждой стороне равностороннего треугольника АВС отложены отрезки АВ₁ = ВС₁ = СА₁ . Точки А₁ , В₁ и С₁ соединены прямыми. Доказать, что треугольник А₁ В₁ С₁ тоже равносторонний.