Курсовая работа: Нестандартные методы решения задач по математике
Ответ: ![]() .
.
Пример 2 Решить уравнение
![]()
Решение. Нетрудно видеть, что ![]() и
и ![]() является корнем уравнения.
является корнем уравнения.
Пусть теперь ![]() , тогда обе части уравнения разделим на
, тогда обе части уравнения разделим на ![]() и получим уравнение
и получим уравнение
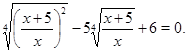
Если обозначить ![]() , то уравнение принимает вид квадратного уравнения
, то уравнение принимает вид квадратного уравнения ![]() , корнями которого являются
, корнями которого являются ![]() и
и ![]() .
.
Рассмотрим уравнения ![]() и
и ![]() , откуда следует, что
, откуда следует, что ![]() и
и ![]() . Так как
. Так как ![]() , то наиденные значения
, то наиденные значения ![]() являются корнями уравнения.
являются корнями уравнения.
Ответ: ![]() ,
, ![]() ,
, ![]() .
.
Пример 3 Решить уравнение
![]()
Решение. Перепишем уравнение в виде
![]()
Положим, что ![]() и
и ![]() , тогда из получим уравнение
, тогда из получим уравнение ![]() , из которого следует
, из которого следует ![]() и
и ![]() ,
, ![]() . Так как
. Так как ![]() и
и ![]() , то
, то ![]() и при этом
и при этом ![]() .
.
Поскольку ![]() и
и ![]() , то
, то ![]() . Отсюда получаем систему уравнений
. Отсюда получаем систему уравнений
![]()
где ![]() . Решением системы уравнений относительно
. Решением системы уравнений относительно ![]() является
является ![]() . Так как при этом
. Так как при этом ![]() и
и ![]() , то
, то ![]() и
и ![]() .
.
Ответ: ![]() .
.
Пример 4 Решить уравнение
![]()
Решение. Для преобразования левой части уравнения воспользуемся очевидным равенством ![]() . Тогда из уравнения имеем
. Тогда из уравнения имеем
![]()
и
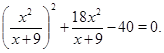
Если затем положить ![]() , то получим уравнение
, то получим уравнение ![]() , корни которого равны
, корни которого равны ![]() и
и ![]() .
.
Таким образом, необходимо рассмотреть два уравнения ![]() и
и ![]() , т.е.
, т.е. ![]() и
и ![]() , где
, где ![]() . Первое уравнение корней не имеет, а из второго получаем
. Первое уравнение корней не имеет, а из второго получаем ![]() .
.
Ответ: ![]() ,
, ![]() .
.
Пример 5 Решить уравнение
![]()