Решение. Поскольку не является корнем уравнения , то разделим обе его части на . Тогда

Если или , то левая часть уравнения будет больше , а правая его часть --- меньше . Следовательно, корни уравнения находятся на отрезке .

Пусть , где . Тогда уравнение принимает вид тригонометрического уравнения

Решением уравнения являются , где --- целое число. Однако , поэтому , и . Так как , то , и .

Ответ: , и .

Пример 9 Решить уравнение

Решение. Нетрудно видеть, что

Выполним замену , где . В таком случае левая часть уравнения принимает вид

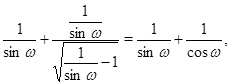
а из уравнения следует тригонометрическое уравнение вида

Сделаем еще одну замену переменных, пусть , тогда и из получаем квадратное уравнение относительно переменной , т.е. , решением которого являются и . Так как и , то и . С учетом того, что , получаем систему тригонометрических уравнений

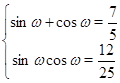
Из уравнений системы составим квадратное уравнение относительно вида и получаем и . Так как , то и

Ответ: , .

Пример 10 Решить систему уравнений

Решение. Поскольку и , то положим и , тогда и . Тогда и . В таком случае , и система уравнений принимает вид

Из первого уравнения системы получаем . Поскольку , то , Следовательно, получаем систему

Отсюда следует и . Так как и , то и .

Ответ: , .

3. Методы, основанные на применении численных неравенств