Курсовая работа: Нестандартные методы решения задач по математике

которое справедливо для произвольных , и натурального числа .

Задачи и решения

Пример 11 Доказать неравенство

где .

Доказательство. Преобразуем левую часть неравенства с использованием неравенства , т.е.

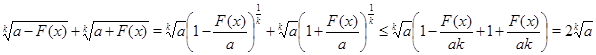
Так как по условию , то равенства в неравенстве Бернулли не будет, поэтому доказано строгое неравенство .

Пример 12 Доказать, что если , то

Доказательство. Введем обозначения и . Тогда и .

Используя неравенство Коши-Буняковского , можно записать . Так как , то и .

Имеет место равенство , из которого следует .

Следовательно, для доказательства неравенства достаточно показать, что или , где .

Пусть . Для доказательства неравенства требуется показать, что , где .

Так как , то корни уравнения являются точками, подозрительными на экстремум функции . Уравнение имеет два корня: , . Поскольку , , , то .

Отсюда следует, что неравенство доказано.

Пример 13 Доказать, если , то

Доказательство. Для получения нижней оценки левой части требуемого неравенства первоначально воспользуемся неравенством Бернулли , а затем неравенством Коши , тогда

Пример 14 Решить уравнение

Решение. Используя неравенство Коши , можно записать

т.е. имеет место неравенство