Курсовая работа: Невласні подвійні інтеграли

передбачити існування скінченної границі

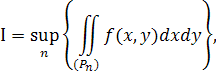
щоб звідси вже випливала збіжність інтеграла (2).

Дійсно, яку б область (Р') не відокремити кривою ( К' ) від (Р), при достатньо великому п ця область цілком буде міститися в ( Р _n ), так що

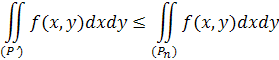
і, тим паче,

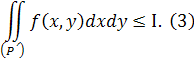
З іншого боку, по заданому >0 можна знайти таке n ₀ , щоб було

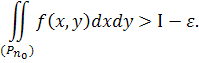
При достатньо великому R , в свою чергу, область (Р') охопить ( ), отже

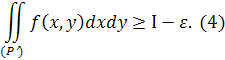
Нерівності (3) і (4) в сукупності доводять, що число І задовольняє визначенню подвійного інтеграла.

Далі, якщо зберегти відносно функції f(x,y) попередні припущення, то із збіжності інтеграла від поширеного на необмежену область (Р) , випливає збіжність подібного ж інтеграла для функції f(x,y).

Для доведення цього розглянемо дві функції:

f ₊ ( x , y ) _, f _- ( x , y ) _;

очевидно,

f ₊ ( x , y )

f _- ( x , y ) =

З інтегрованості функції випливає збіжність інтегралів для функцій

f ₊ ( x , y ) f _- ( x , y )

а отже, і для функції

f ( x , y )= f ₊ ( x , y )- f _- ( x , y )

Вельми чудовий той факт, що і навпаки: із збіжності інтеграла від функції f(x,y), поширеного на необмежену область (Р), випливає збіжність інтеграла і для Цьому твердженню немає аналога в теорії одновимірних невласних інтегралів: відомо, що можуть існувати і інтеграли, що не абсолютно збіжні.

Теорема про абсолютну збіжність невласного подвійного інтеграла. Кожнийзбіжний інтеграл

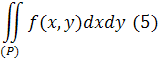
необхідно і абсолютно збіжний, тобтоодночасно з нимзбіжний і інтеграл

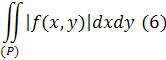
Для доведення цієї теореми будемо користуватись методом доведення від супротивного. Візьмемо послідовність областей {(Р _n ) }, так, щоб вони, розширюючись, поступово охоплювали всю область (Р), матимемо

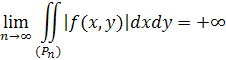
Ми можемо припустити, що при кожному значенні п виконується нерівність

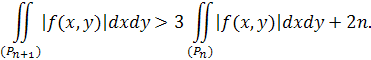
Цього можна досягти, розріджуючи (в разі потреби) послідовність {(Р _n ) }, тобто витягуючи з неї часткову послідовність і заново нумеруючи її.