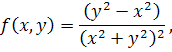Курсовая работа: Невласні подвійні інтеграли

Вочевидь, умови збіжності будуть:

(а)m<1, (б) m>1, (в) m<1.

2) Аналогічне питання по відношенню до інтегралів ()

Вказівка. Вдатися до підстановки

Відповідь. (а) (б) (в)

Ті ж відповіді вийдуть і у разі, коли зміна змінних в задачах 1), 2) обмежується сектором між променями θ = θ₀ і θ = θ₁ .

3) Якщо область (D₁ ) зміни змінних х ,y криволінійний трикутник АОВ, обмежений відрізком АO осі х , дугою ОВ параболи y = х² і дугою ВА кола x ² + y ² = 1, то інтеграл

для якого початок як і раніше слугує особливою точкою, все ж існує (хоча не існує для круга!). Дійсно, при переходідо полярних координат інтеграл утворюється до вигляду

звідки і витікає сказане.

4) Аналогічно, взявши за область трикутник АОС (той же малюнок), можна встановити існування інтеграла

для якого особливими будуть точки А і С . Так як в полярних координатах рівняння лінії АС буде , то запропонований інтеграл зводиться до наступного:

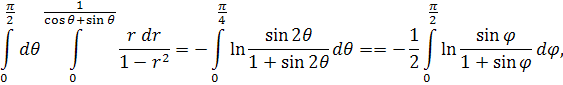
який явно існує.

5)На порівнянні з інтегралами, розглянутими в 1),ґрунтується наступна ознака збіжності:

Якщо ( D ) є: (а) обмежена область, що містить початкову точку, або (б) область, що тягнеться в нескінченність, не містить початкової точки, то інтеграл від функціїf ( x , y ) в ( D ) збігається, оскільки f ( x , y ) в ( D ) може бути представлена у вигляді

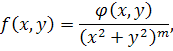
де обмежена і, відповідно випадку,(а) т< 1 або (б) m >1.

Легко перефразувати цю ознаку для випадку, коли початкова точка замінена будь-якою точкою (х₀ , у₀ ).

6) Перевірити збіжність подвійного інтеграла від функції