Курсовая работа: Невласні подвійні інтеграли
Через ![]() позначений кут променя OB зполярною віссю.
позначений кут променя OB зполярною віссю.
Відповідь. У випадках (а), (г) інтеграл не сходиться (тим більше це справедливо для випадків (б)і(д)!); у випадку (в) інтеграл збігається, він рівний![]()
7) Подвійний інтеграл
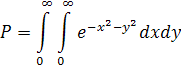
існує,або існує повторний:
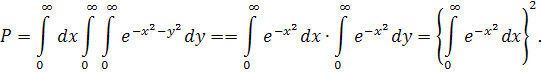
Його легко обчислити, якщо перейти до полярних координат; перший квадрант, на площині ху перетвориться при цьому в смугу на площині r![]() обмежену прямими
обмежену прямими ![]() = 0, r = 0 і
= 0, r = 0 і ![]() =
= ![]() . Таким чином,
. Таким чином,
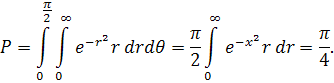
Тому, що
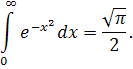
Відповідь. Інтеграл рівний ![]() .
.
Висновок
У цій курсовій роботі розглянуто означення і основні властивості невласного подвійного інтеграла, особливості і відмінності від інших визначених інтегралів.
Вказані задачі приводять до двох пов'язаних між собою видів інтегралів: невизначеного і визначеного. Вивчення властивостейі обчислення цих інтегралів і складають основну задачу інтегрального. числення. Введений визначений інтеграл як границя інтегральних сум, передбачаючи при цьому, що відрізок інтегрування скінченний, а інтегральна функція на цьому відрізку обмежена. Якщо хоча б одна з цих умов порушувалась, то наведене вище означення визначеного інтеграла стає неприйнятним: у випадку нескінченного проміжку інтегрування його не можна розбити на п частинних відрізків скінченної довжини, а у випадку необмеженої функції інтегральна сума явно не має скінченної границі. Узагальнюючи поняття визначеного інтеграла на ці випадки, приходимо до невласного інтеграла — інтеграла від функції на необмеженому проміжку або від необмеженої функції.
За допомогою курсової роботи ми навчилися визначати умови існування, методи, способи обчислення невласних подвійних інтегралів і розглянули деякі приклади. Отже, можемо стверджувати, що невласні подвійні інтеграли є самостійним інструментом для розв’язку певного класу задач.
Список літератури
1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001. - 648 с. .: іл.: іл.
2. Шкіль М. І. Математичний аналіз: Підручник: У 2ч. Ч.1- 3-тє вид., переробл. і доповн. – К .: Вища шк.. , 2005. – 447с.: іл.
3. Фіхтенгольц Г. М. Основи математичного аналізу. Том 1:Учебник. – М.:Печатный двор, 1957г. – 440с.:илл.
4. Фихтенгольц Г. М. Курс дифференциального и интегрального исчесления. Том 3: Учебн. пособиэ. – М.: Наука, 1969г. – 656с.:илл.
5. Лиман В.Ф., Власенко В.Ф., Петренко С.В., Одінцова О.О., Семеніхіна О.В. Вища математика: Навч. посібник. У2 ч. – Суми: ВТД «Університетська книга», 2005. – 614с.:іл.
6. Кудрявцев Л.Д. Курс математического анализа, т.2. ![]() М.: Высшая школа, 1965. – 369с
М.: Высшая школа, 1965. – 369с
7. Градштейнб Рыжик И.М. Таблицы интегралов, сумм, рядовпроизведений.![]() М.: Наука, 1963 – 312с.
М.: Наука, 1963 – 312с.
8. Давидов М.О. Курс математчного анализу. Ч. 1. – К.:Вища школа, 1990. – 350с.
9. Канторович Л.В., Акилов Г.Л. Функциональный анализ. – М.: ИЛ, 1961 – 321с.