Курсовая работа: Невласні подвійні інтеграли

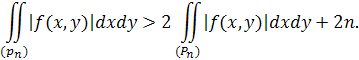
Але

| f ( x , y )|= f ₊ ( x , y )+ f _- ( x , y ),

Отже

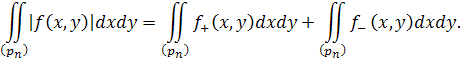
Нехай з двох інтегралів з права більшим буде, наприклад, перший. Тоді

Замінюючи подвійний інтеграл зліва досить близькою до нього нижньою сумою Дарбу, збережемо нерівність

В цій сумі залишаємо лише ті доданки, яким відповідають

позначивши сукупність відповідних елементів через ( )_, отримаємо,

Позначимо через (P ̃ _n ) область, складену з (Р _n ) і ( р̃ _n ); такяк

то, складаючи почленно цю нерівність з попередньою, знайдемо

Область (р̃ _n ), а з нею і (Р̃ _n ), можна деформувати так, щоб з останньої вийшла зв'язна область (Р' _n ), і притому за площею, що настільки мало різниться від (Р̃ _n ), що все ж зберігається нерівність

Цього легко досягти, сполучаючи відірвані частини області вузькими «коридорами» з довільно малою загальною площею.

Звідси вже ясно, що інтеграл (5) не може бути збіжним, всупереч припущенню; це протиріччя і доводить теорему.

Відмітимо, що принципова різниця між одновимірним і двовимірним випадками пов'язана саме із завершальною частиною проведеного міркування. Незв'язну лінійну область, що складається з окремих проміжків, вже не можна довільно малою деформацією перетворити в цілісний проміжок.

Доведена теорема зводить питання про збіжність і обчислення невласного інтеграла від довільної функції до такого ж питання для додатної (від’ємної) функції.

Інтеграли від необмежених функцій.

Нехай функція f ( x , y ) задана в обмеженій області (Р), але сама виявляється необмеженою в околі окремих точок М_1, М_2,… в будь - якій частині області (Р), що не містить цих точок.

Виділимо тепер особливі точки М_1, М_2,… оточивши їх кривими (К ₁ ), (К ₂ ) , ... Якщо видалити з області (Р) обмежені цими кривими околи особливих точок, то ми отримаємо область (Р'), для якої по припущенню інтеграл

є збіжний. Будемо «стягувати» криві ( К ₁ ) ,( K ₂ ), ... у вказані точки так, щоб найбільша з відстаней точок цих контурів (К) до відповідних точок M (позначимо її через ρ) прямувала до нуля . Відмітимо, що при цьому і площі даних околів (менші ніж πρ² ), також прямуватимуть до нуля.

Інтеграл ( невласний ) від необмеженої функції f(x, y ) по області (Р) визначається як границя інтеграла (7) при ρ→0:

Особливі точки можуть лежати і уздовж деяких особливих ліній, які ми завжди будемо передбачати такими, що мають площу 0. В цьому випадку доводиться оточувати ці лінії околами, що «стискуються» до них.