Курсовая работа: Определение дуальных и двойных чисел

. (8)

Здесь есть модуль числа , а отношение называется аргументом этого числа и обозначается через Arg z (r может быть произвольным вещественным числом, отличным от нуля; - произвольным вещественным числом). Очевидно, что вещественные числа характеризуются равенством нулю их аргумента; сопряжённые дуальные числа и имеют одинаковый модуль r и противоположные аргументы и .

Форма (8) записи дуальных чисел очень удобна в тех случаях, когда эти числа приходится перемножать или делить. Действительно,

; (9)

следовательно, модуль произведения двух дуальных чисел равен произведению модулей сомножителей[1] , а аргумент произведения - сумме аргументов. Отсюда вытекает, что модуль частного двух дуальных чисел равен частному модулей этих чисел, а аргумент частного – разности соответствующих аргументов:

. (10)

Наконец, из этих правил выводятся также и законы, позволяющие возвышать дуальное число в любую степень и извлекать из него корень:

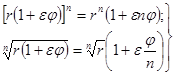(11)

(из последней формулы вытекает, что корень нечётной степени из дуального числа при определяется однозначно; корень же чётной степени не существует, если r <0, и имеет два значения, еслиr >0[2] ).

1.2 Двойные числа

В полной аналогии со всем изложенным выше назовём двойные числа и сопряжёнными, если они имеют вид

и .

Сумма и произведение сопряжённых двойных чисел вещественны; корень квадратный из числа , знак которого совпадает со знаком большего по абсолютной величине из вещественных чисел a и b , называется модулем числа и обозначается через . Легко проверить, что для двойных чисел остаются в силе все формулы (3); кроме того, ясно, что равенство характеризует вещественные числа , а равенство - чисто мнимые числа .

Сложение, вычитание, умножение и деление двойных чисел определяются формулами

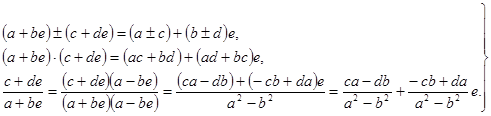(12)

Отсюда следует, что и здесь деление на возможно лишь в тех случаях, когда . Двойные числа , модуль которых равен нулю, называются делителями нуля (заметим, что ). В некоторых случаях оказывается удобным считать частные , и числами новой природы; при этом оказывается необходимым ещё расширить понятие двойного числа, введя дополнительно произведения и новых чисел и на всевозможные вещественные числа c и частные и . Правила действия над символами , , , и определяются формулами (5) и рядом соотношений, родственных (6), например:

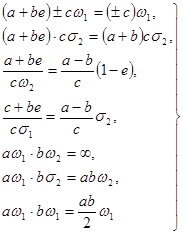(13)

и т. д. Естественно также положить

, , , , (13а)

что обеспечит выполнение для расширенного указанным образом множества двойных чисел равенства и всех соотношений (3).

Двойные числа ненулевого модуля можно также записать в форме, аналогичной форме (8) записи дуальных чисел. Пусть - модуль двойного числа; далее

.

Из определения модуля следует, что и что большая (по абсолютной величине) из дробей и положительна. Отсюда вытекает, что

, или , , (14)

где есть некоторое число (определённое формулами (14)), а и – гиперболический косинус и гиперболический синус аргумента .

Таким образом, имеем

или . (15)

величина называется аргументом двойного числа z и обозначается через Arg z [3] .

Форма (15) записи двойных чисел очень удобна в тех случаях, когда приходится перемножать два или несколько двойных чисел. Действительно, из формул сложения гиперболических функций следует, что