Курсовая работа: Определение дуальных и двойных чисел

, (23)

где , , , .

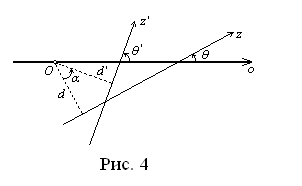
Перейдём теперь к вращениям плоскости. Очевидно, что поворот вокруг O на угол переводит прямую в прямую , где (рис. 4). Таким образом,

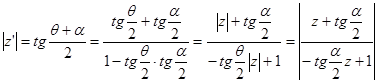(24)

(здесь используется то, что если z иz – дуальные числа, то , и 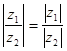). Далее, если d иd ′– расстояния прямых z иz ′ отполюса , то

поэтому

.

С другой стороны, поскольку , то

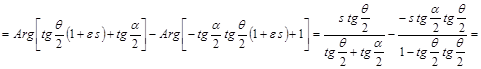
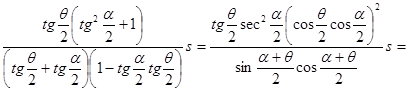
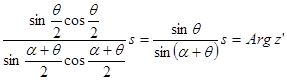. (24а)

Из (24) и (24а) следует, что наше вращение записывается формулой

, (25)

где , .

Наконец, самое общее движение представляет собой поворот (25) вокруг O на некоторый угол , причём это вращение может сопровождаться ещё параллельным переносом (33):

.

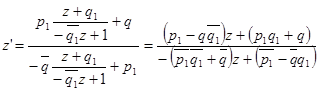В другом виде это преобразование можно записать так:

, (26а)

где , .

Возможно, также, что исходное движение представляет собой симметрию (21б) относительно прямой o , сопровождаемую преобразованием (36а) (вращением вокруг O и параллельным переносом):

. (26б)

Наконец, движение может представлять собой переориентацию (21в), сопровождаемую одним из преобразований (36а) или (36б):

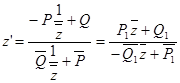, (26в)

где , , или

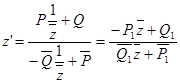, (26г)

где , .

Очевидно, что ориентированный угол {} между прямыми и равен (рис. 5, а)