Курсовая работа: Определение дуальных и двойных чисел

Это можно записать так:

.

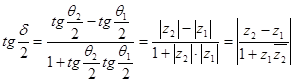Полученный результат можно также представить в следующей симметричной форме:

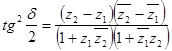. (27)

Найдём теперь ориентированное расстояние d ={[],[]} между точками [] и [] пересечения определённой прямой с двумя другими прямыми и (рис. 5, б). Очевидно, что расстояние d между точками пересечения прямой o с прямыми и равно

.

Пример движения, переводящего данную прямую в прямую o , даётся формулой

;

это движение переводит прямые и в прямые и . Отсюда получаем

.(28)

Условием того, что прямые , и пересекаются в одной точке, является равенство нулю расстояния между точками пересечения и с , т.е., в силу формулы (28), вещественность отношения .

Это условие можно переписать ещё так:

. (29)

Следовательно, “уравнение точки”, т.е. условие, которому удовлетворяют прямые , проходящие через одну точку [], имеет вид

,

или

, A – чисто мнимое (30)

(здесь , ).

Найдём теперь условие того, что четыре ориентированные точки , , и принадлежат одной ориентированной окружности. При этом под ориентированной окружностью мы здесь понимаем совокупность всех ориентированных прямых l , ориентированное расстояние {O , l } которых от данной точки O (центра окружности) имеет фиксированное значение r . Число r называется радиусом окружности; таким образом, радиус ориентированной окружности может быть как положительным, так и отрицательным. Из определения ориентированного расстояния {O , l } от точки O до прямой l следует, что радиус ориентированной окружности будет положительным, если направление обхода противоположно направлению вращения часовой стрелки, и отрицательным в противном случае.

Можно показать, что четыре ориентированные прямые , , и в том и только в том случае принадлежат одной ориентированной окружности или проходят через одну точку, если

{[],[]}{[],[]}={[],[]}{[],[]}. (31)

Чтобы убедиться в этом, рассмотрим рис. 33, на котором изображены четыре ориентированные касательные , , и ориентированной окружности S , касающиеся S соответственно в точках M ,N ,P иQ ; точки [], [], [] и [] обозначены через A , B , C иD . При этом, очевидно, имеем

{A ,B }{C ,D }={A ,P }{P ,B }{C ,Q }{Q ,D }

и

{D ,A }{B ,C }={D ,M }{M ,A }{B ,N }{N ,C }

В силу известного свойства касательных к окружности

{A ,P }={M ,A }, {P ,B }={B ,N }, {C ,Q }={N ,C }, {Q ,D }={D ,M },

значит, во всех случаях выполняется условие (31)

{A ,B }{C ,D }={D ,A }{B ,C }.