Курсовая работа: Определение дуальных и двойных чисел

Таким образом, модуль произведения двух двойных чисел равен произведению модулей сомножителей, а аргумент произведения – сумме аргументов; при этом произведение имеет первую или вторую из форм (15) в зависимости от того, имеют ли сомножители одну и ту же или разные формы. Из формул (16) сразу вытекают правила деления двойных чисел:

;

. (17)

Из формул (16) получаются также правила, позволяющие возводить двойное число в любую целую положительную степень n и извлекать из него корень степени n :

,

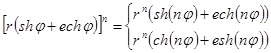
при

n нечётном,

при n чётном;

Глава II .

2.1 Дуальные числа как ориентированные прямые плоскости.

Две ориентированные прямые будем называть параллельными лишь в том случае, если они параллельны в обычном смысле и направления этих прямых совпадают (рис. 1, а); параллельные прямые противоположных направлений будем называть противопараллельными (рис. 1, б).

а б

Рис. 1

Под расстоянием от прямой a до не пересекающей её прямой b будем понимать ориентированное расстояние {a , b } от a до b , т.е. ориентированное расстояние от произвольной точки прямой a до прямой b ; очевидно, что {a , b }=- {b , a }, если a иb параллельны, и {a , b }={b , a }, если a и b противопараллельны.

Полярные координаты точек плоскости определяются заданием некоторой точки O (полюса системы координат) и проходящей через O ориентированной прямойo (полярной оси); координатами точки M служат расстояние r = OM этой точки от полюса и угол ={o , m }, образованный с o ориентированной прямой m , соединяющей O иM . Аналогично этому можно определить полярные координаты ориентированных прямых плоскости, для задания которых надо также указать некоторую ориентированную прямую o (полярную ось) и лежащую на o точку O (полюс); координатами прямой l служат угол ={o , l }, образованный l с полярной осью o , и ориентированное расстояние s = {O , L } от O до точки L пересечения l и o (рис. 2,а). Очевидно, что координатаs ориентированной прямой l может иметь любое значение, заключённое между и ; координата – любое значение, заключённое между 0 и 2. Естественно считать, что =0 для прямых, параллельных полярной оси o , и = для прямых, противопараллельных o ; если прямая не пересекает оси o , то координаты s она не имеет (можно считать, что в этом случае ).

Условимся сопоставлять ориентированной прямой l с полярными координатами и s дуальное число

, , (19)

(рис. 2). При этом параллельным o прямым, для которых =0, естественно относить числа нулевого модуля, т.е. делители нуля . Чтобы установить точное соответствие между параллельными o прямыми и делителями нуля, заметим, что расстояние d = {O , l } не параллельной o прямой l от полюса O равно

(20)

(рис. 2, а). Чтобы формула (20) сохранила силу и для параллельной o прямой m , отстоящей от o на расстоянии {o , m }= d , то этой прямой нужно сопоставить число

(т.е. , где u = 0 и ).

Двум пересекающим o прямым l и l , отличающимся только направлением и, следовательно, имеющим полярные координаты () и (), отвечают дуальные числа

и