Курсовая работа: Определение основных характеристик системы передачи сообщений с дискретной фазовой модуляцией

4. Энтропия – это математическое ожидание количества информации или мера неопределенности сообщений.

При заданном законе распределения мгновенных значений процесса a(t) все уровни квантования равновероятны. Для этого найдем вероятность j-го уровня квантования, что равносильно вероятности попадания a(t) в интервал .

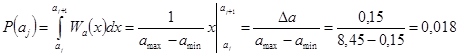
Видно, что не зависит от j.

Тогда энтропия будет определяться как энтропия дискретного источника независимых сообщений, все символы которого вероятны:

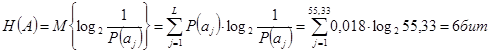
Производительностью такого источника будет суммарная энтропия сообщений, переданных за единицу времени:

5. Кодер

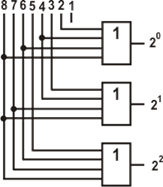
Шифратор (кодер) – это устройство, представляющее собой преобразователь позиционного кода в двоичный. В позиционном коде число определяется позицией единиц в серии нулей, или позицией нуля в серии единиц. Например, если в серии десять нулей, имеется вот такой код 0001000000, то это эквивалентно числу 7 (счет ведется справа налево от нуля). Такой код служит для включения объектов или передачи данных на них. Для преобразования позиционного кода в двоичный составим таблицу 5.1:

Рис. 5.1 Реализация шифратора на логических элементах

Таблица 5.1

Позиционный код								Двоичный код
8	7	6	5	4	3	2	1	22	21	20
0	0	0	0	0	0	0	1	0	0	0
0	0	0	0	0	0	1	0	0	0	1
0	0	0	0	0	1	0	0	0	1	0
0	0	0	0	1	0	0	0	0	1	1
0	0	0	1	0	0	0	0	1	0	0
0	0	1	0	0	0	0	0	1	0	1
0	1	0	0	0	0	0	0	1	1	0
1	0	0	0	0	0	0	0	1	1	1

Для наглядности, единицы, как видно, располагаются по диагонали. Единице соответствуют единицы в позиционном коде, соответствующие числам 2, 4, 6, 8 (разрядам). Следовательно, эти разряды объединяются через схему ИЛИ. Аналогичные операции проходят над старшими разрядами. В результате получим рис. 5.1:

Примечание: разряд 1 так и висит в воздухе, как на схеме. Согласно таблице, ей соответствует код 000.

В кодере процесс кодирования осуществляется в два этапа. На 1-ом этапе производится безызбыточное (примитивное) кодирование каждого уровня квантованного сообщения a(t₁ ) к -разрядным двоичным кодом. На 2-ом этапе к полученной к -разрядной двоичной кодовой комбинации добавляется один проверочный символ, формируемый простым суммированием по модулю 2 всех информационных символов. В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют нулевым символам кодовой комбинации, а отрицательные – единичным.

Требуется:

1) Определить минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(t₁ ).

2) Определить избыточность кода с одной проверкой на четность Р_к .

3) Записать двоичную кодовую комбинацию, соответствующую передаче a_j -го уровня, считая, что при примитивном кодировании на 1-м этапе a_j -му уровню ставится в соответствие двоичная кодовая комбинация, представляющая собой запись числа в двоичной системе.

4) Определить число двоичных символов, выдаваемых кодером в секунду V_к и длительность двоичного символа Т.

1. Найдем минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(t₁ ).

2. Определим избыточность кода с одной проверкой на четность.

3. Представим число j =46 в двоичной системе счисления:

Следовательно к-6 информационных символов кодовой комбинации будут иметь вид:

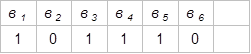Определим проверочный символ в₇ путем суммирования по модулю 2 всех к=6 информационных символов

Учитывая, что правило суммирования по модулю 2 имеет вид: