Курсовая работа: Определение основных характеристик системы передачи сообщений с дискретной фазовой модуляцией

Рис. 6.2. Функция корреляции

3. Найдем выражение для спектральной плотности мощности модулированного сигнала по теореме Винера-Хинчина:

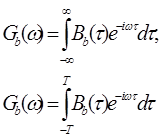
Так как B_b (τ) – функция четная, то

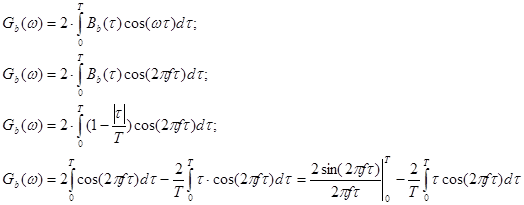
Возьмем интеграл 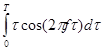по частям:

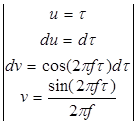
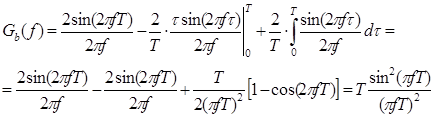
Построим график спектральной плотности мощности модулирующего сигнала:

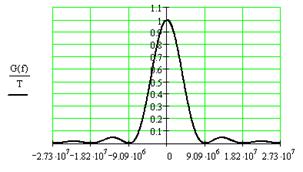
Рис. 6.3. График спектральной плотности мощности модулирующего сигнала

4. Найдем условную ширину спектра сигнала. Под условной шириной спектра сигнала понимают полосу частот, в которой сосредоточена основная доля мощности сигнала. Чем больше выбранное значение α, тем большая доля мощности будет сосредоточена в этой полосе частот.

Пусть α=2

Определим долю мощности, сосредоточенную в полосе частот от 0 до .

;

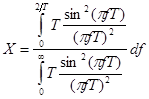
Рассмотрим по отдельности числитель и знаменатель этого выражения.

Возьмем этот интеграл по частям:

-интегральный синус;

Аналогично получим, что

То есть получили, что 95% всей мощности сигнала приходится на полосу частот от 0 до .

5. После перекодировки последовательности и в(t) в последовательность C(t) по правилу нулевому символу соответствует , единичному – . В дальнейшем происходит модулирование сигнала s(t) по правилу:

Пусть , тогда

При , тогда , следовательно