Курсовая работа: Определение основных характеристик системы передачи сообщений с дискретной фазовой модуляцией

Таким образом, искомая кодовая комбинация, соответствующая передаче а ₅₅ уровня квантованного сообщения, будет иметь вид:

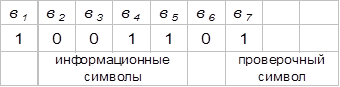
4. Число двоичных символов, выдаваемых кодером в секунду , определяется числом отсчетов (1/Δt) и числом двоичных символов n=k+1, приходящихся на один отсчет.

Длительность двоичного символа определяется как величина, обратная

6. Модулятор

В модуляторе синхронная двоичная случайная последовательность биполярных импульсов в(t) осуществляет манипуляцию гармонического переносчика U₀ cos(2πf₀ t).

Параметры несущей:

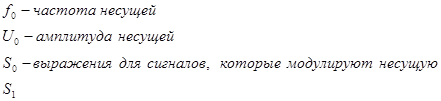
U₀ =1B,

f₀ =100V_k =100*9,09*10=909 МГц;

;

.

Требуется:

1. Изобразить временные диаграммы модулирующего и манипулированного сигналов, соответствующих передаче -го уровня сообщения .

2. Привести выражение и начертить график корреляционной функции модулирующего сигнала .

3. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала .

4. Определить условную ширину энергетического спектра модулирующего сигнала из условия (где выбирается от 1 до 3). Отложить полученной значение на графике .

5. Записать аналитическое выражение модулированного сигнала .

6. Привести выражение и построить график энергетического спектра модулированного сигнала .

7. Определить условную ширину спектра модулированного сигнала . Отложить полученное значение на графике .

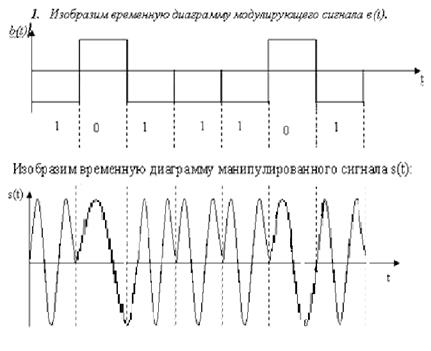
Рис. 6.1. Временные диаграммы модулирующего и монипулированного сигналов

2 . Для определения функции корреляции рассмотрим два сечения в моменты t₁ и t₂ , (t₂ – t₁ =τ) и найдем математическое ожидание произведения X(t₁ ) X(t₁ + τ).

Если τ>Т, то эти сечения принадлежат разным тактовым интервалам и произведение может с равной вероятностью принимать значения +1 и -1, так что его математическое ожидание равно 0.

Если τ <Т, то возможны два варианта: случай А, когда они принадлежат одному интервалу и, следовательно, X(t₁ ) X(t₁ + τ)=1, и случай В, когда они принадлежат разным таковым интервалам и X(t₁ ) X(t₁ + τ) может с равной вероятностью равняться +1 и -1. Поэтому при τ <Т математическое ожидание X(t₁ ) X(t₁ + τ) равно вероятности р(а) того, что оба сечения оказались в одном интервале. Случай А имеет место, если первое из двух сечений отстоит от начала тактового интервала не более чем Т-, а вероятность этого равна (Т-)/Т.

Тогда функция корреляции имеет вид: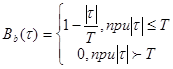

В()